本文探讨了参数化复杂度理论，它通过引入参数 k 来细化分析算法的复杂度，并揭示了问题结构对算法难度的影响。作者以贝叶斯网络推理为例，展示了参数 k 如何捕捉问题的本质结构，并解释了树宽这一参数在贝叶斯网络推理中的意义。

📈 **参数化复杂度理论：** 通过引入参数 k，将问题的输入进行分层，使得算法复杂度在固定 k 的情况下为多项式，而仅在 k 上呈指数增长。这有助于更细致地分析问题的结构，理解哪些因素导致特定实例的难度。 例如，在贝叶斯网络推理中，可以通过树宽 k 来衡量网络中变量之间相互作用的程度。树宽越低，推理的复杂度越低。 该理论可以应用于许多 NP 完备问题，并揭示了这些问题在实际应用中可能并不像理论分析中那样难解。

📊 **贝叶斯网络推理的复杂度分析：** 作者以贝叶斯网络推理为例，展示了参数化复杂度的应用。 通过分析贝叶斯网络的结构，可以发现一些特定结构的网络（例如链状结构）可以实现线性时间推理。 作者进一步引入了树宽的概念，并解释了树宽如何体现网络中变量之间相互作用的程度，从而影响推理的复杂度。

📉 **参数化复杂度与实际应用：** 参数化复杂度理论为理解问题的结构提供了新的视角，并有助于解释为什么一些 NP 完备问题在实际应用中并不难解。 例如，自然界中的问题可能具有较低的树宽，这使得人类可以有效地进行推理和决策。 该理论也为算法设计提供了新的思路，可以通过优化参数 k 的值来提高算法的效率。

Published on July 3, 2024 7:06 PM GMT

Tl;dr, While an algorithm's computational complexity may be exponential in general (worst-case), it is often possible to stratify its input via some dimension $k$ that makes it polynomial for a fixed $k$, and only exponential in $k$. Conceptually, this quantity captures the core aspect of a problem's structure that determines what makes specific instances more difficult than others, often with intuitive interpretations.

Example: Bayesian Inference and Treewidth

One can easily prove exact inference (decision problem of: "is $P\left(X\right)>0$?") is NP-hard by encoding SAT-3 as a Bayes Net. Showing that it's NP is easy too.

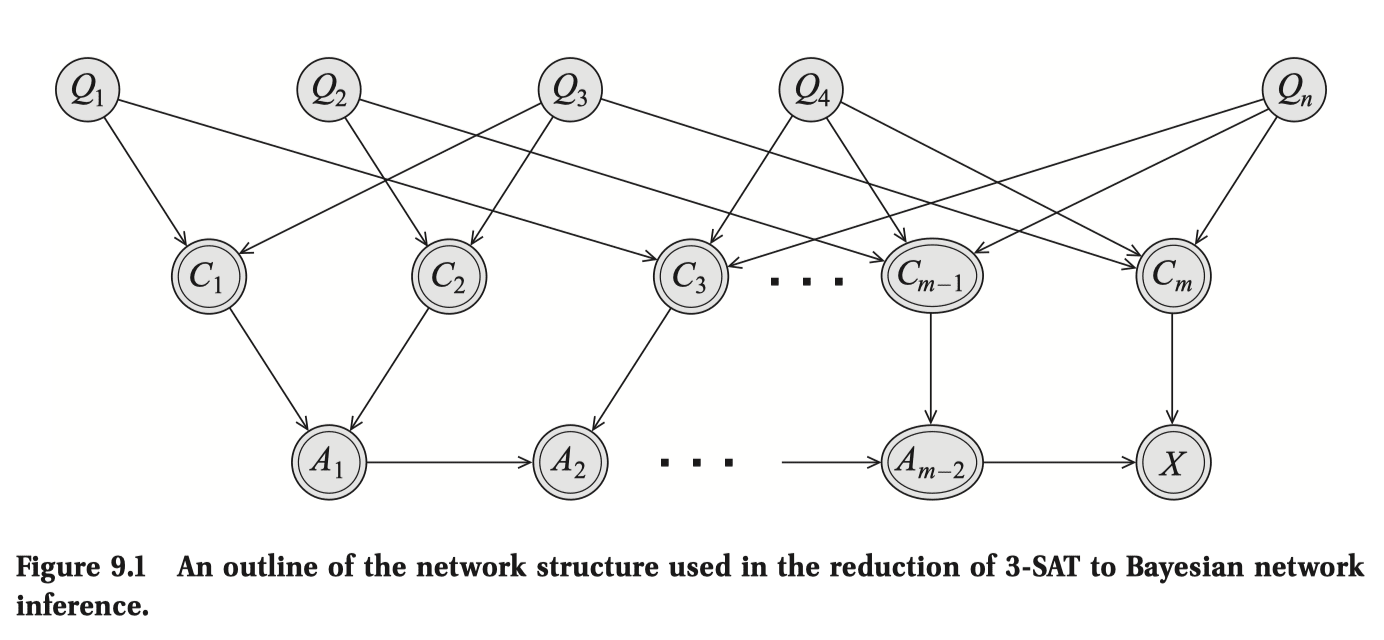
Therefore, inference is NP-complete, implying that algorithms are worst-case exponential. But this can't be the typical case! Let's examine the example of a Bayes Net whose structure is a chain  $A⟶B⟶C⟶D,$ and say you want to compute the marginals $P\left(D\right)$.

The Naive Algorithm for marginalization would be to literally multiply all the conditional probability distribution (CPD) tables for each of the Bayes Net's nodes, and sum over all the variables other than $X$. If we assume each variable has at most $v$ values, then the computational complexity is exponential in the number of variables $n$.

$P\left(D\right)={\sum }_A{\sum }_B{\sum }_{C}P(A,B,C,D)$, which is $O\left(v^n\right)$.

But because of the factorization $P(A,B,C,D)=P\left(A\right)P\left(B|A\right)P\left(C|B\right)P\left(D|C\right)$ due to the chain structure, we can shift the order of the sum around like this:

$P\left(D\right)={\sum }_{C}P\left(D|C\right){\sum }_{B}P\left(C|B\right){\sum }_{A}P\left(A\right)P\left(B|A\right)$

and now the sum can be done in $O\left(n{v}^2\right)$. Why?

Notice ${\sum }_{A}P\left(A\right)P\left(B|A\right)$ is $P\left(B\right)$, and to compute $P(B=b)$ we need to multiply $v$ times and sum $v-1$ times, overall $O\left(v\right)$.This needs to be done for every $b$, so $O\left(v^2\right)$. Now we have cached $P\left(B\right)$, and we move on to ${\sum }_{B}P\left(C|B\right)P\left(B\right)$, where the same analysis applies. This is basically dynamic programming.

So, at least for chains, inference can be done in linear time in input size.

The earlier NP-completeness result, remember, is a worst-case analysis that applies to all possible Bayes Nets, ignoring the possible structure in each instance that may make some easier to solve than the other.

Let's attempt a more fine complexity analysis by taking into account the structure of the Bayes Net provided, based on the chain example.

Intuitively, the relevant structure of the Bayes Net that determines the difficulty of marginalization is the 'degree of interaction' among the variables, since the complexity is exponential in the "maximum number of factors ever seen within a sum," which was 2 in the case of a chain.

How do we generalize this quantity to graphs other than chains?

Since we could've shuffled the order of the sums and products differently (which would still yield $O\left(n{v}^2\right)$ for chains, but for general graphs the exponent may change significantly), for a given graph we want to find the sum-shuffling-order that minimizes the number of factors ever seen within a sum, and call that number $k$, an invariant of the graph that captures the difficulty of inference — $O\left(m{v}^k\right)$^[1]

This is a graphical quantity of your graph called treewidth^[2][3].

So, to sum up:

We've parameterized the possible input Bayes Nets using some quantity $k$.Where $k$ stratifies the inference problem in terms of their inherent difficulty, i.e. computational complexity is exponential in $k$, but linear under fixed or bounded $k$.We see that $k$ is actually a graphical quantity known as treewidth, which intuitively corresponds to the notion of 'degree of interaction' among variables.

---

General Lesson

While I was studying basic computational complexity theory, I found myself skeptical of the value of various complexity classes, especially due to the classes being too coarse and not particularly exploiting the structures specific to the problem instance:

The motif of proving NP-hardness by finding a clever way to encode SAT-3 is a typical example of problem-structure-flattening that I'm troubled by.

But while studying graphical models, I learned that, there are many more avenues of fine-grained complexity analyses (after the initial coarse classification) that may lend real insight to the problem's structure, such as parameterized complexity.

While many algorithms (e.g., those for NP-complete problems) are exponential (or more generally, superpolynomial) in input size in general (worst-case), there are natural problems whose input can be stratified via a parameter $k$ - whose algorithms are polynomial in input size given a fixed $k$, and only exponential in $k$.

This is exciting from a conceptual perspective, because $k$ then describes exactly what about the problem structure makes some instance of it harder or easier to solve, often with intuitive meanings - like treewidth!

Also, I suspect this may shed light on to what makes some NP-hardness results not really matter much in practice^[4] - they don't matter because natural instances of the problem have low values of $k$. From this, one may conjecture that nature has low treewidth, thus agents like us can thrive and do Bayes.

1. ^{^}

   $m$ is the number of times the sum was performed. In the case of chains, this was simply $n-1$, thus $O\left(n{v}^2\right)$. I omitted m because it seemed like an irrelevant detail for conveying the overall lesson.

2. ^{^}

   A graphical quantity of your undirected graph by turning all the directed edges of the Bayes Net to undirected ones.

3. ^{^}

   Actually, $k-1$ is treewidth. Trees (which chains are an example of) have a treewidth of 1, thus $k=2$.

4. ^{^}

   Among many other reasons also laid out in the link, such as use of approximations, randomization, and caring more about average / generic case complexity. My point may be considered an elaboration of the latter reason.

Discuss