Published on April 21, 2025 3:21 PM GMT
In our earlier post, we described how one could parametrize local image patches in natural images by a surface called a Klein bottle. In Love et al, we used this information to modify the convolutional neural network construction so as to incorporate information about the pixels in a small neighborhood of a given pixel in a systematic way. We found that we were able to improve performance in various ways. One obvious way is that the neural networks learned more quickly, and we therefore believe that they could learn on less data. Another very important point, though, was that the new networks were also able to generalize better. We carried out a synthetic experiment on MNIST, in which we introduced noise into MNIST. We then performed two experiments, one in which we trained on the original MNIST and evaluated the convolutional models on the “noisy” set, and another in which we trained on the noisy set and evaluated on the original set. The results are displayed below.
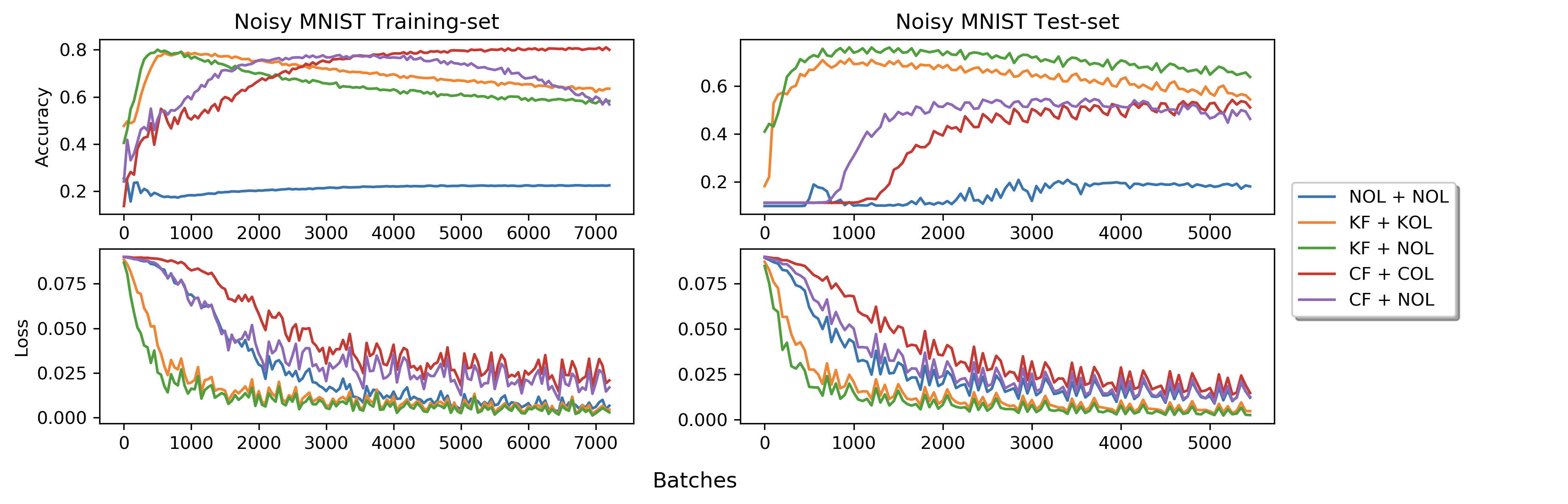
The upper boxes describe the accuracy on the test set, while the lower boxes show training loss. The orange, green, purple, and red curves belong to various versions of the networks which have been modified to incorporate the Klein bottle information, and the blue curve is a standard convolutional neural network. The left column describes the results when training on the noisy set and evaluating on the original MNIST, and the right the results when using the original MNIST for training and evaluating on the noisy set. It is clear that the Klein networks outperform standard CNN’s dramatically on generalization in this setting. We also considered generalization from one data set to another.
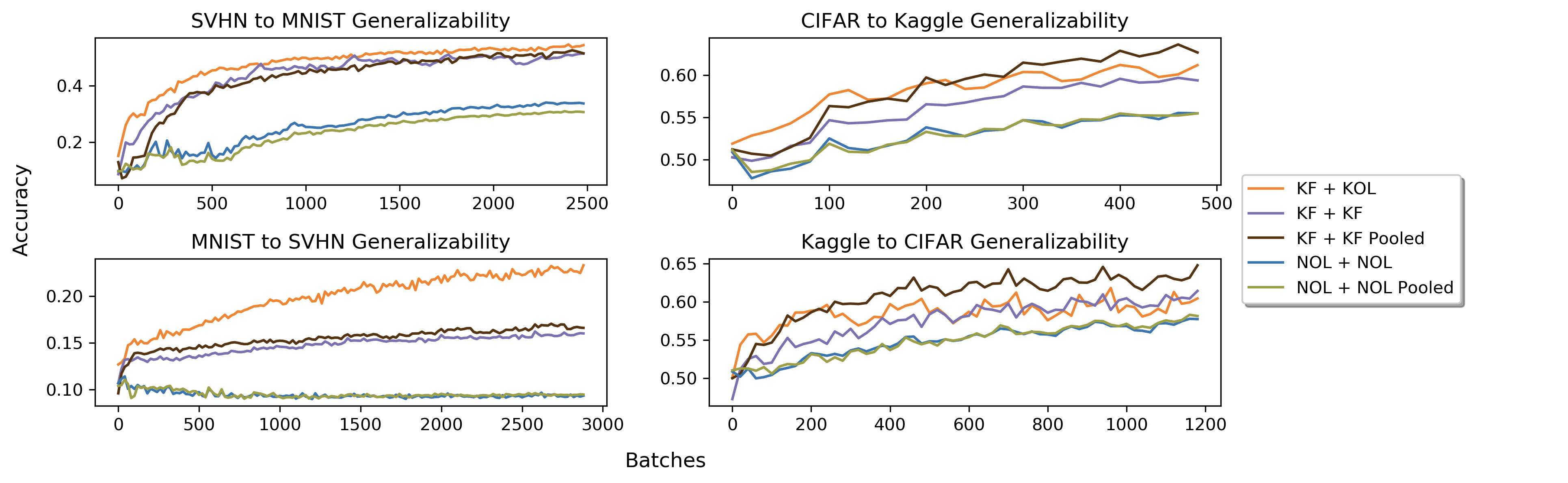
The curves on the left describe generalization from the SVHN data set of pictures of house numbers to MNIST, and vice versa. In this case, the orange, purple, and brown curves describe the performance of three different versions of the Klein modified constructions, while the green and blue describe two different versions of standard CNN architectures, one with pooling and one without. On the right, you see generalization between CIFAR and Kaggle data sets, for the question of classifying cats vs. dogs. In both cases, the Klein modified networks outperform standard constructions on generalization.
The ability to generalize is a very important criterion for assessing the quality of an AI model. What these results have demonstrated is that it is possible to improve generalization by performing a kind of knowledge injection into the AI model, in this case the knowledge being the understanding of local patch behavior for natural images.
A question asked by the authors of Love et al was whether or not this knowledge and understanding could suggest something useful for video classification. We return to the Klein bottle, and recall how the patches are parametrized by it.
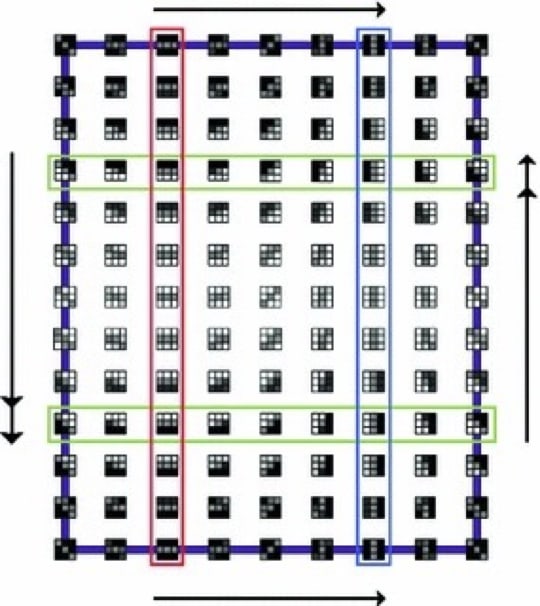
Let’s consider the horizontal rows outlined in green. You can see that as you traverse the upper row from left to right, we achieve a rotation of 180 degrees. The Klein bottle (lets call it ) has identifications which identify the right hand endpoint of the upper row with the left hand endpoint of the lower row. As we move from left to right along the lower row, we continue to rotate until we achieve a 360 degree rotation. Note that this is consistent since the right hand endpoint of the lower row is identified with the left hand endpoint of the upper row. So, in conclusion, rotation of the patches is achieved by moving along a circle laid out horizontally in . On the other hand, let’s look at the five middle patches in the vertical column outlined in blue.

What appears to be happening is that a solid region is moving from left to right, starting out concentrated on the left hand side, then moving so that it becomes a vertical line in the middle of the box, and then moves to the right until we have a solid region on the right hand side. This can be thought of as approximately translating from left to right. In summary it appears that movements in the horizontal directions correspond to rotations of patches, while movement in the vertical direction can be roughly interpreted as translation. Movements in intermediate directions, like 45 degrees, will reflect a combination of the two. Nevertheless, what this analysis suggests is the possibility that interesting features for the analysis of video could be “infinitesimal movements” in , what we might think of as tangent directions in . There is a mathematical construction that you can apply to any surface or manifold , called the unit tangent bundle to , and is denoted by , which consists of pairs , where is a point of and is a unit length vector tangent to the surface. For the circle, this is a very simple construction.

In the picture, we illustrate some points in the tangent bundle to the circle Remember, each such point is a pair consisting of a point on the circle and a tangent direction at that point. So, we have the north, south, east, and west “poles” on the circle, and each one has associated with it two directions, a blue one and a red one. We have by no means shown all the points on , only eight of them. For any angle , we will have two points on , one for the blue direction and one for the red. This means that as a space, will consist of two subsets, each of which is a circle. One piece will consist of the red clockwise unit directions, and the other will consist of the blue counterclockwise unit directions.

Each point on the red circle represents the corresponding point on the circle above paired with the clockwise direction, and each point on the blue circle will represent the corresponding point on the circle paired with the counterclockwise direction.
Since is two-dimensional, the different unit length directions do not consist of only two points, but instead of a full circle. For that reason, the unit tangent bundle of is actually 3-dimensional, 2 for itself, and one for the unit directions, which form a circle. It is a relatively complicated space, but can be coordinatized with three intrinsic coordinates, analogous to the intrinsic coordinate for the circle or the two intrinsic coordinates for .
The point of this is that in Love et al,, the tangent bundle to the Klein bottle is used to build a modified 12 layer ResNet for video classification tasks. The difference between our modified version and an ordinary 12 layer ResNet was evaluated on a data set from the University of Central Florida of videos taken on human activities such as baby crawling, playing cello, and swinging a tennis racket. The results are given in the figure below.
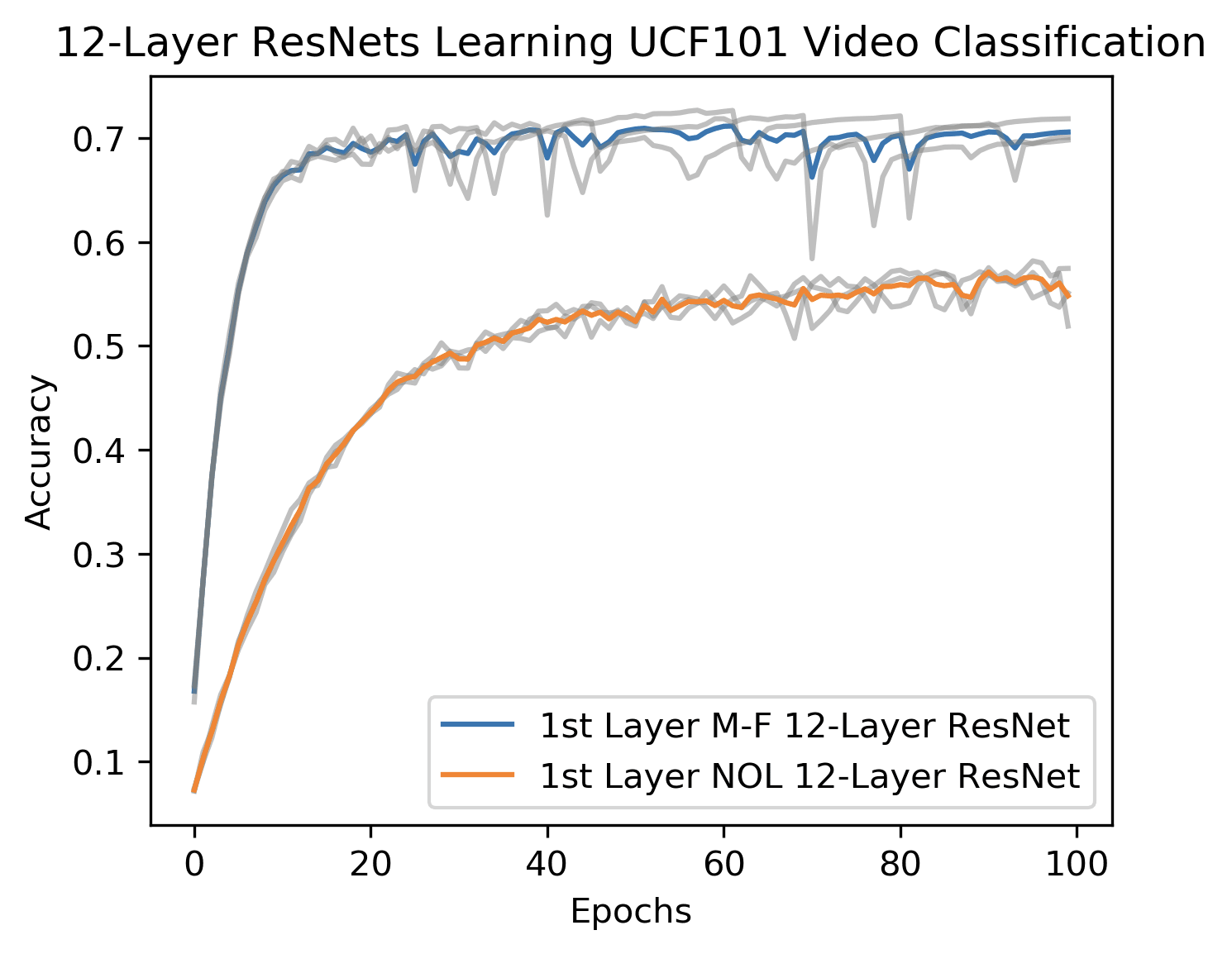
The curves track the accuracy of the models vs. the number of training epochs, with the blue curve associated with our topological model and the orange curve a standard ResNet. As you can see, the learning is much more rapid with the topological model, and the final result for the is also much better (~70% vs. ~52%). In Love et al, other data sets were studied, both from the point of view of accuracy and speed but also generalization. In all cases, the topologically constructed network evidenced a substantial improvement over the standard ResNet.
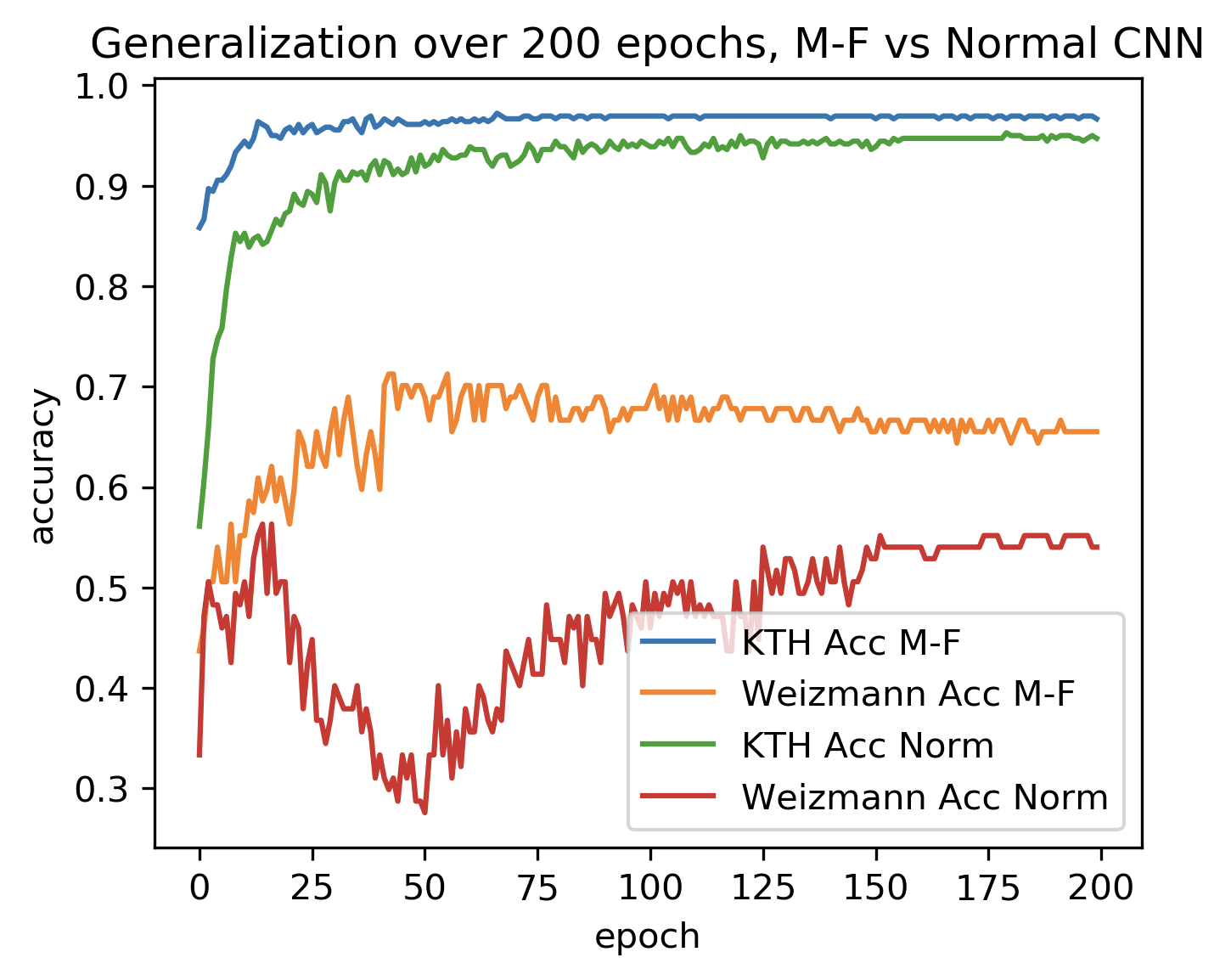
Above you see the results from training on a data set of human motions from KTH and evaluating on an analogous data set from the Weizmann institute. The upper two curves indicate the training accuracy over epochs while the lower two indicate accuracy on the test set (Weizmann). The orange and blue curves are topologically modified, while the green and red are standard ResNets. On the test set, the accuracy of the topologically modified model is ~65% while the standard model achieves ~52%.
We remark that we restricted the topological model to a subset of the tangent bundle, so as to have the size of the network to be reasonable. Other versions of this construction would likely lead to further improvement.
The point we want to make is twofold.
- Interpreting and understanding the topology of spaces of features attached to data sets can yield constructions which perform better than standard techniques, and that improvement includes the important property of generalization. Interpretability can also allow one to reason about possible architectures and methodologies, without having to collect any data. Our understanding of still images suggested a natural hypothesis about what would improve video classification, and that hypothesis turned out to be correct. The idea is that interpretability and understanding permits us to make educated guesses or even "leaps of faith" about what might improve AI models.
Discuss

