Title: Contrastive Deep Nonnegative Matrix Factorization For Community Detection

Paper Link: https://arxiv.org/pdf/2311.02357

https://ieeexplore.ieee.org/abstract/document/10446107

Code: https://github.com/6lyc/CDNMF

今天给大家分享中山大学GTML实验室以及Inpluslab发表在ICASSP 2024上的一篇论文【Contrastive Deep Nonnegative Matrix Factorization for Community Detection】。近年来，非负矩阵分解（Non-negative Matrix Factorization, NMF）因其较好的可解释性被广泛应用于社区检测任务。然而，现有的基于NMF的方法普遍存在以下三个问题：1）它们直接将原始网络映射到社区成员空间，因此难以捕捉网络的层次信息；2）它们通常只关注网络的拓扑结构，而忽略了节点的属性；3）它们难以学习社区检测所需的全局结构信息。因此，研究者提出了一种新的社区检测算法——基于对比模式的深度非负矩阵分解算法（Contrastive Deep Nonnegative Matrix Factorization, CDNMF）。首先，通过深度化NMF算法来增强其信息提取能力。随后，受对比学习的启发，该算法创新性地将网络拓扑和节点属性构建为两个对比视图。此外，利用去偏负采样层在社区级别学习节点间相似性，从而增强了模型对社区检测任务的适用性。该论文在多个图数据集上进行了实验。相比于其他社区检测方法，在准确率上至少提升3-6%。同时验证了对比模式的有效性和算法训练的高效性。

1 研究背景

社区检测（Community Detection）是复杂网络分析中的一项基本任务。它目的是将网络划分为多个子结构，每个子结构对应一个社区。有效的划分要求同一社区内的节点密集连接，而不同社区之间的节点连接稀疏。挖掘社区结构是揭示和理解复杂网络系统组织原则和运行机制的关键。例如，在社交网络中，平台通过检测不同的用户社区来促进好友推荐和广告投放。除了在社交网络中的应用外，社区检测还广泛应用于蛋白质-蛋白质相互作用（PPI）网络、引文网络等。

在过去的二十年中，学术界提出了许多经典算法用于社区检测，例如模块度 (modularity)、电导 (conductance)和持久性 (permanence)。然而，这些方法只能将每个节点分配到一个社区，从而限制了其在现实场景中的适用范围。近年来，基于神经网络的方法逐渐成为该领域的主流，比如GUCD和VGAER。然而，它们的训练过程是一个黑盒，导致结果的可解释性有限。进一步的，研究人员提出了基于NMF的社区检测算法，由于其良好的数学可解释性和自然适用于重叠社区检测，得到了广泛应用。在进行重叠社区检测时，可以根据分解因子矩阵V将每个节点分配到几个倾向较高的社区。此外，还有一些性能更好的NMF变体，例如正交非负矩阵分解（ONMF）、贝叶斯非负矩阵分解（BNMF）、非负矩阵三分解（NMTF）和MX-ONMTF等。

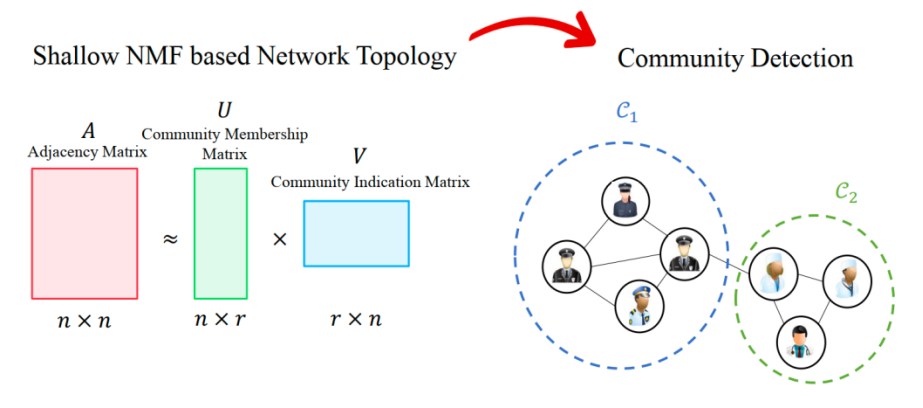
然而，这些基于NMF的方法仍然存在以下三个问题：

这些方法是浅层，通常只有单层或双层的映射，难以提取现实世界网络的结构。

这些方法往往只关注网络的拓扑结构，而忽略了节点的属性。在社会科学中，研究表明节点属性可以反映并影响其社区的结构。

这些方法无法捕捉网络中的社区级别信息。基于NMF的方法关注相邻节点之间的相似性，难以提取社区检测所需的全局结构信息。

本文提出了一种新的社区检测算法CDNMF，以解决现有方法的局限性。主要贡献如下：

提出使用深度NMF（Deep NMF）作为骨干模型，以增强算法的表示学习能力。

构建了一个对比学习框架，基于DNMF统一学习图拓扑和节点属性。此外，通过分解结果以及去偏负采样层过滤掉错误负样本，使模型更好地学习社区级别的信息。

进行了广泛的实验，以评估CDNMF的优越性、有效性和效率。

2 方法

CDNMF由三个模块组成，模型的总体框架如下图所示。

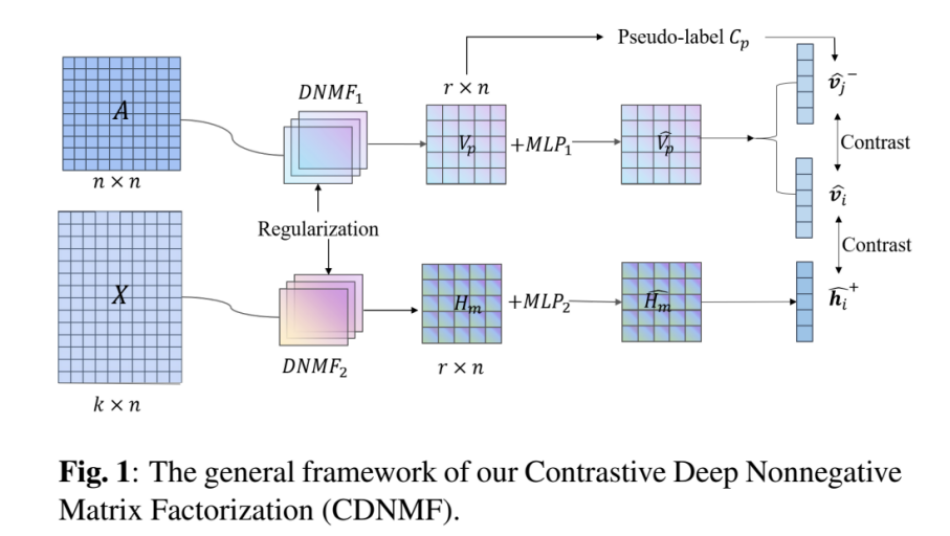
2.1 DNMF层

为了从原始网络拓扑中提取层次信息，将邻接矩阵A重构为深度形式：

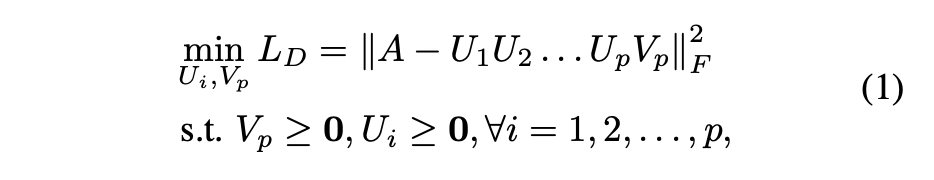
每个矩阵Ui可以解释为具有不同层次信息的第i个特征矩阵。U1U2...Un 是原始网络与社区成员空间之间的总映射。矩阵Vp是经过深度变换后的节点表示矩阵，每一列可以理解为一个节点属于不同社区的倾向。

为了将带有约束的优化问题（1）转换为无约束问题，为每个非负矩阵设计了一个惩罚项。首先，定义函数 f满足：

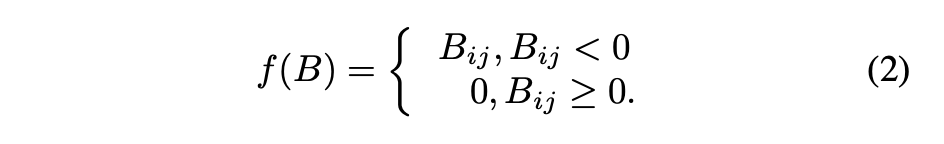
简而言之，函数f用于将输入矩阵的正元素转换为0，而保持负元素不变。矩阵 Ui (i=1,2,...,p)的惩罚项定义为：

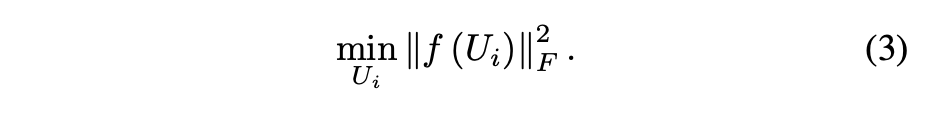
将优化问题（1）转换为以下无约束目标函数：

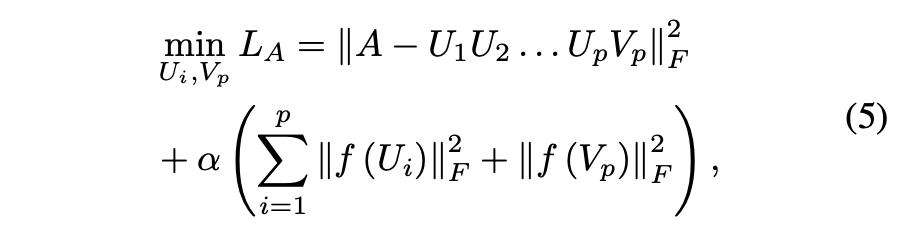
总体而言，得到了DNMF项的目标函数：

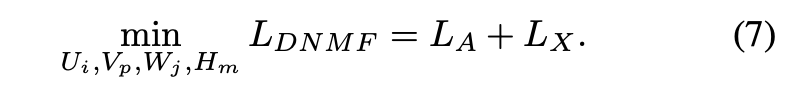
此外，为了在深度层次映射中保留节点对的固有几何结构，引入了图正则化：

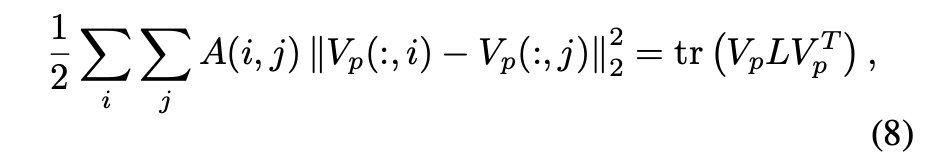
其中L=D-A表示图拉普拉斯矩阵, D是对角矩阵，其对角线元素是A的行和。tr(·)表示矩阵的迹。

然后，对两个视图都最小化图正则，并得到图正则化项的目标函数：

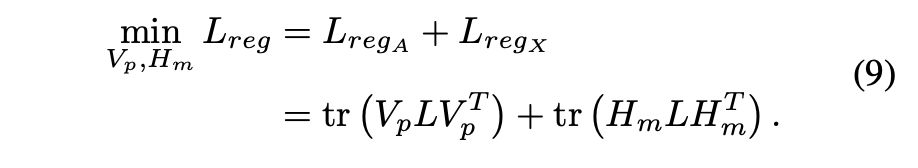
2.2 去偏负采样层

通过DNMF层可以直接从节点表示矩阵中获得伪社区标签，减少错误的负样本。首先通过以下方式获得节点vi的伪标签：

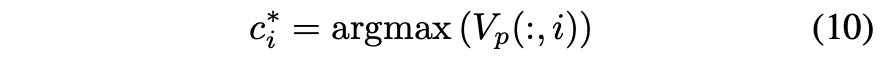
接下来，移除所有与vi具有相同伪标签的节点，以获得该节点的去偏负样本集：

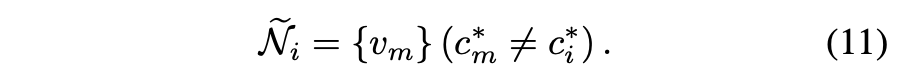
事实上，伪社区标签的准确性会随着训练迭代次数的增加而不断提高。

2.3 图对比学习层

研究者使用网络拓扑的邻接矩阵A和节点属性的特征矩阵X作为对比学习的两个视图。特别是，对于每个节点vi，将拓扑视图上生成的表示向量Vp(:,i)作为锚点，将节点属性视图上生成的表示向量Hm(:,i)作为正样本，并将式(11)中集合的节点表示向量作为负样本。

然后，对于每个正样本对[Vp(:,i), Hm(:,i)]，定义对比损失如下：

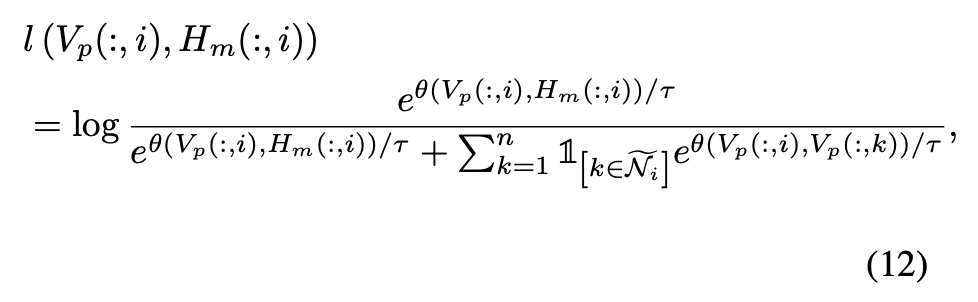
正样本的对比提取了每个节点拓扑和属性的一致性和互补信息。负样本的对比扩大了不同社区之间的距离，使本文的模型能够学习节点之间的社区级别相似性。

在图对比学习层中，优化每个节点的对比损失，并得到对比学习项的目标函数：

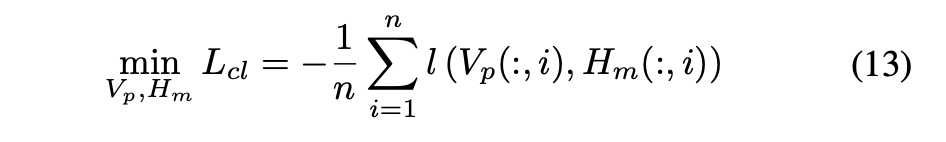
2.4 训练过程

联合优化每一层，并定义总目标函数如下：

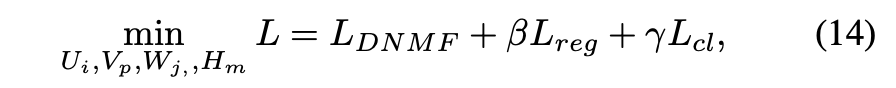
在算法1的训练过程之后，每个节点的预测社区标签为：

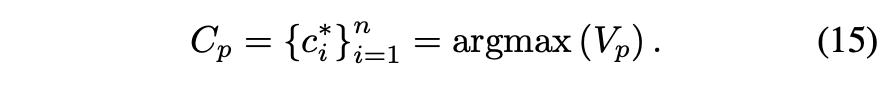
3 实验

3.1 社区检测

表1展示了模型在社区检测任务中的表现。

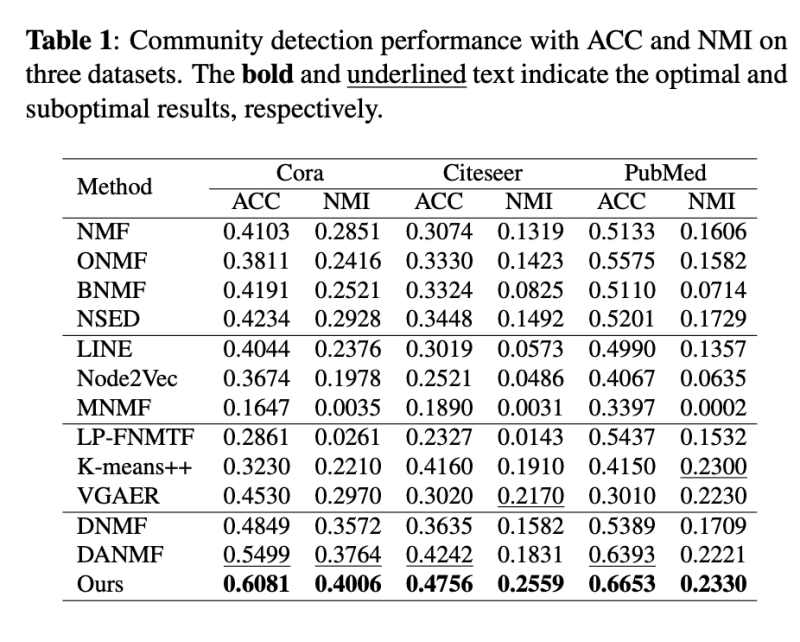
3.2 消融实验

表2展示了图数据的两种信息（拓扑结构以及节点属性）对社区检测的重要性。

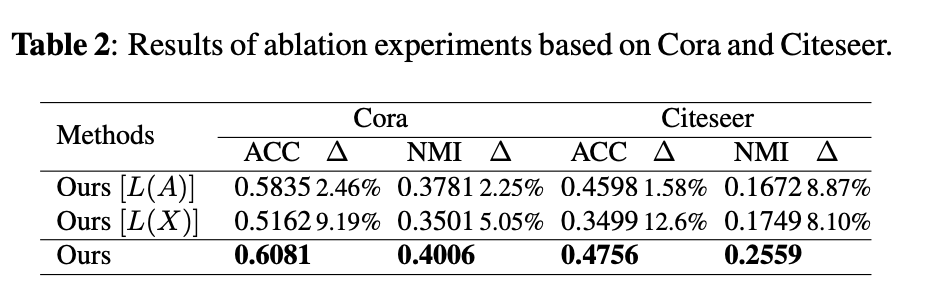
3.3 收敛性分析

下图展示了本文算法的收敛速度。

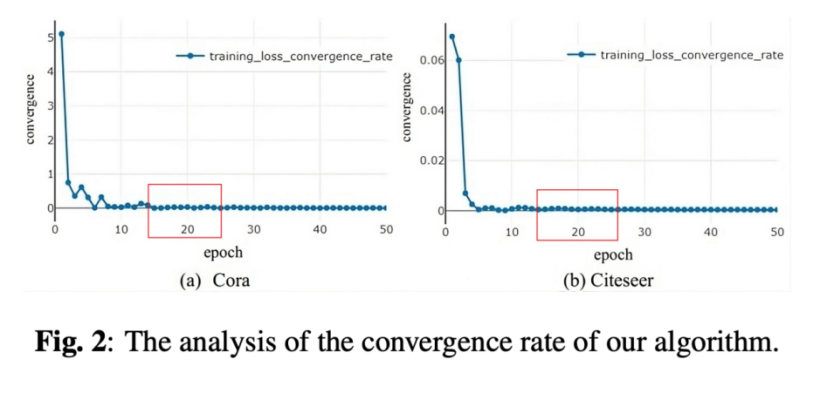
4 结论

本文提出了一种新的社区检测方法CDNMF，具有良好的可解释性以及卓越的效果。该框架首次将NMF与对比学习进行结合，它们之间是相互促进并自然耦合的。一方面引入对比学习，其中正样本的对比是为了让NMF算法可以同时学到图的拓扑信号和属性信号，同时负样本的对比可以让NMF输出更适合社区检测的嵌入空间。另一方面，NMF也被引入本文的框架，借助其输出结果可以在对比学习中得到更精确的负样本，其次还增加模型的可解释性。此外，还可以考虑结合不同的矩阵分解方式（例如ONMF，BNMF，DANMF等）以及对比学习算法（例如MVGRL，GRACE等），在CDNMF框架下进一步衍生出其他兼具可解释性和效用的社区检测算法！