Max Tegmark组新工作：利用调和损失训练可解释的AI模型

摘要

在本文中，我们提出了一种新的损失函数调和损失（Harmonic Loss），作为标准交叉熵损失（cross-entropy loss）的替代方案，用于训练神经网络和大规模语言模型（LLMs）。调和损失由于其尺度不变性和有限收敛点的设计，使得模型具有更强的可解释性并实现更快的收敛，其中有限收敛点可以被解释为类别中心。我们首先在算法任务、计算机视觉任务和自然语言处理任务上验证了 Harmonic Loss 的性能。通过一系列实验，我们证明了采用调和损失训练的模型在以下几个方面优于标准模型：(a) 提高可解释性，(b) 降低对大量训练数据的依赖，(c) 减少 grokking 现象（延迟泛化）。此外，我们对比了采用 Harmonic Loss 训练的 GPT-2 与标准 GPT-2，结果表明 Harmonic Loss 使模型能够学习到更具可解释性的表示。展望未来，Harmonic Loss 有望成为数据受限领域或高风险应用场景（如医疗、金融）中的重要工具，促进更稳健、高效的神经网络模型的发展。

Max Tegmark也曾受邀在集智俱乐部分享：构建可控、可解释的AI系统：https://pattern.swarma.org/study_group_issue/503

研究领域：调和损失、可解释性、神经网络、通用化、grokking现象、大语言模型

论文题目：Harmonic Loss Trains Interpretable AI Models
发表时间：2025年2月3日
论文地址：https://arxiv.org/abs/2502.01628

近年来，神经网络和大型语言模型（Large Language Models, LLMs）的广泛应用极大地改变了人们的生活。然而，这些模型在通用化能力上仍面临着可解释性、数据效率和grokking现象等挑战。近期Max Tegmark组提出了一种新的损失函数——调和损失（Harmonic Loss），作为传统交叉熵损失的替代方案，可显著提高大模型的可解释性和训练效率。

文章共同第一作者刘子鸣在集智俱乐部就神经标度律做过相关报告，揭示大模型的预测能力随着更多的数据和更大的模型而幂律提升这一现象，其背后的理论和对AI+Science带来的启发。
回看地址：https://pattern.swarma.org/study_group_issue/446?play_start_time=425
以及作为24年爆火的全新深度学习网络结构KAN架构的提出者，刘子鸣本人在集智俱乐部对其工作进行了深入解读，感兴趣者可加入AI+Science读书会。
回看地址：https://pattern.swarma.org/study_group_issue/668

调和损失的原理与优势

本文提出了一种新的损失函数调和损失，用于训练神经网络和大语言模型。传统的损失计算使用的交叉熵损失，核心计算的是内积，并进行Softmax归一化；而调和损失函数计算则使用欧几里得距离替代内积，并通过Harmonic Softmax进行归一化，作为向量相似性度量。从而提高模型的可解释性、数据利用效率，并减少延迟泛化（grokking）现象。

调和损失具有两大核心数学特性：尺度不变性和有限收敛点。Harmonic Loss 具有尺度不变性，即当输入向量整体缩放时，模型的损失值和优化方向保持不变，从而提高训练的稳定性。相比于传统交叉熵损失需要将 logits 推向无穷大才能达到确定性分类，Harmonic Loss 依赖于有限收敛点，使得模型在训练过程中能够更快收敛，并获得更加紧凑和可解释的特征表示。

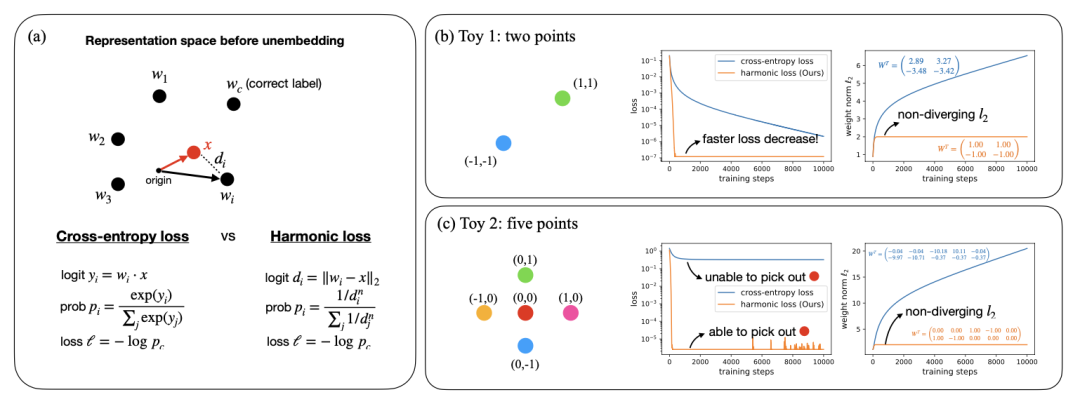
图 1. 交叉熵损失与调和损失。(a) 定义：交叉熵损失利用内积作为相似性度量，而调和损失使用欧几里得距离。(b) 玩具模型1：有2个的点（类）。调和损耗和L2范数在调和损耗下收敛得更快。(c) 玩具模型2：有5个点（类）。调和损失可以挑出中间的红点，而交叉熵损失不能，因为红点与其他点不能线性分离。加权矩阵在调和损失下比在交叉熵损失下更易于解释。

实验方法与结果

研究首先利用算法数据集进行测试，共使用 5 个任务：上下文学习（In-Context Learning），模块化加法（Modular Addition），等价类判定（Equivalence Classes），家谱推理（Genealogy Learning），排列组合（Permutation Composition），比较标准 MLP、标准 Transformer、Harmonic MLP 和 Harmonic Transformer 模型的表现。调和损失在所有任务上均学习到了更紧凑的低维结构，并且数据利用效率更高，需要更少的数据即可达到相同的泛化性能。调和损失的引入还减少了模型 Grokking现象，例如，在模块化加法任务中，标准 MLP 需要 10⁵ 轮训练才能泛化，而 Harmonic MLP 仅需 10³ 轮训练。

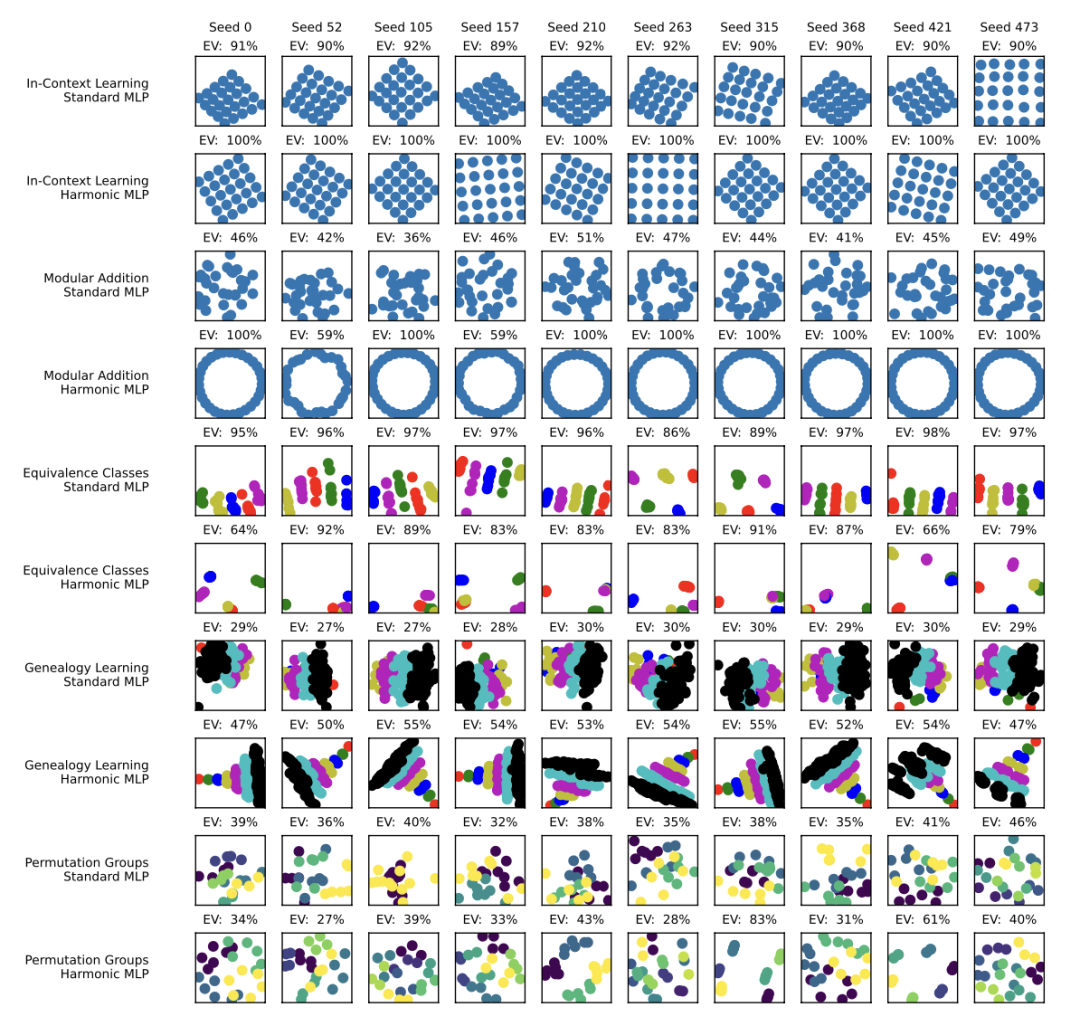
图 2. 综合测试中嵌入的前两个主成分的可视化。每个子图的标题显示了前两个主成分所解释的方差。每行对应一个数据集和一个模型的组合，而每列代表使用不同随机种子进行的不同训练运行的嵌入。连续的两行属于同一个数据集，模型按以下顺序排列：{标准多层感知机，调和多层感知机}。数据集的顺序如下：{上下文学习，谱系学习，等价类，模块化加法和置换群}。X 轴和 Y 轴的跨度相等。

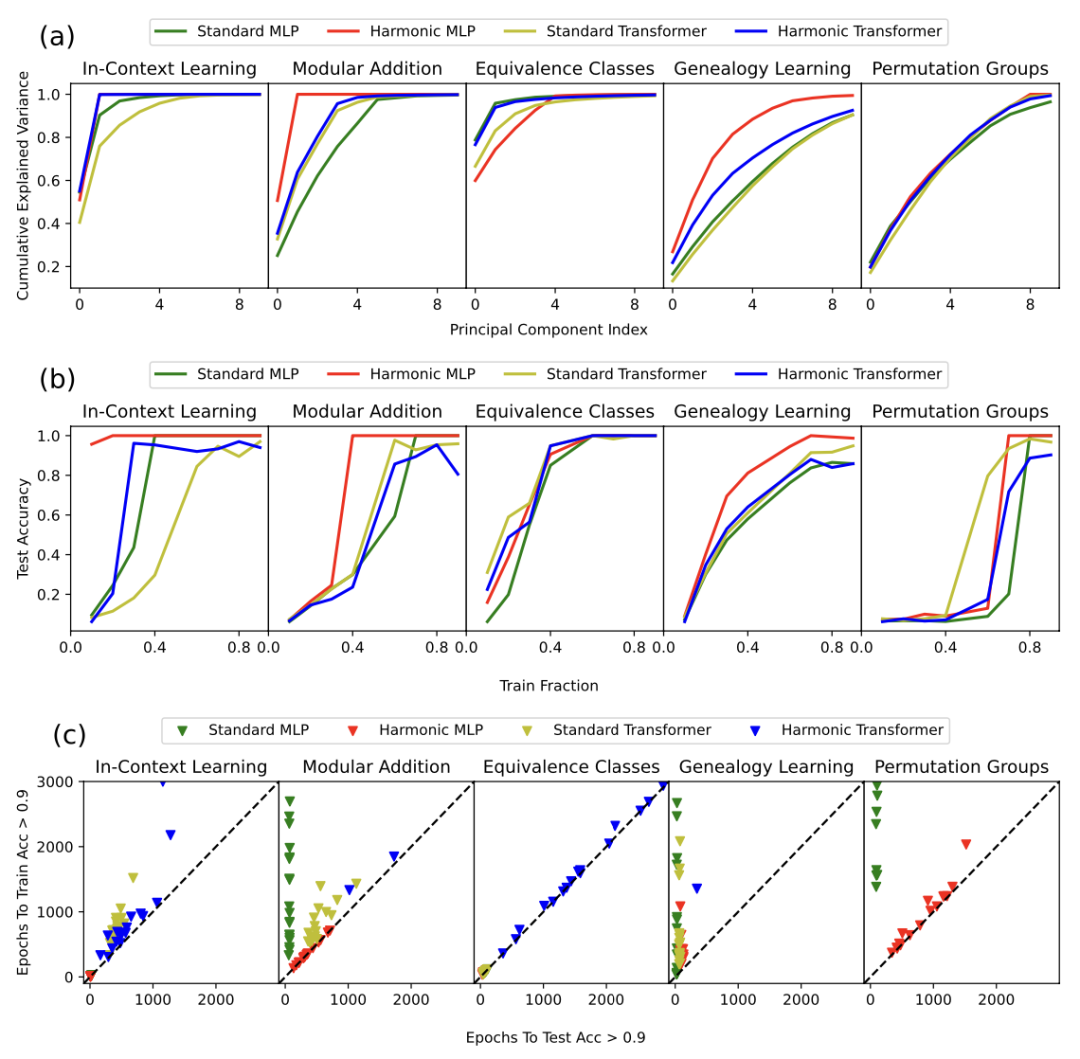
图 3.（a）主成分函数的累积解释方差（20 个种子的中位数）。调和表示比标准表示更紧凑。（b）训练比例函数的测试准确率。调和模型在数据更少的情况下比标准模型更快地泛化。（c）测试准确率＞0.9 所需的轮次与训练准确率＞0.9 所需的轮次（连续 20 次）。y = x 线表示没有grokking，即训练准确率和测试准确率同时提高。靠近 y 轴的点表示掌握程度更高。绘制了 20 个不同随机种子的结果，未能达到 90%准确率的测试被省略。

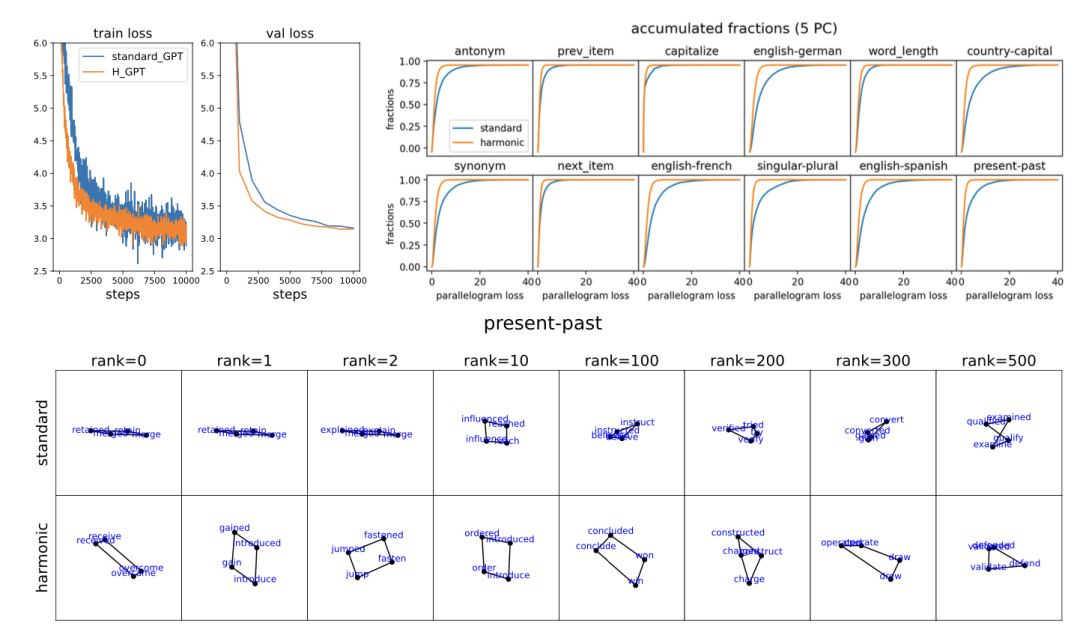
在MNIST的实验中，使用调和损失的简单神经网络能够学到更加可解释的特征，显示出与类别中心对齐的权重分布，这表明调和损失在视觉任务中同样有效。而在大语言模型GPT-2的实验中，研究表明，调和损失训练的GPT-2 训练速度更快，具有更好的可解释性，并且性能不逊于标准 GPT-2。在可解释上，研究采用 “present-past”（动词时态转换）任务进行测试，调和损失训练的GPT-2模型在生成的表示上更优，生成的词向量呈现更规则的平行四边形结构，而标准 GPT-2 生成的词向量呈现扁平的、形状不规则的结构，暗示调和损失能捕捉到更深层次的语言模式。

图 4. GPT2 实验，基于 OpenWebText 训练了 10000 步。（左上角）损失曲线。Harmonic GPT 达到的损失略低于标准 GPT。（右上角）针对十二个函数向量任务的平行四边形损失的累积分布函数。Harmonic GPT 一直表现出更低的平行四边形损失（即更好的平行四边形）。（底部）按质量从左到右降序排列的平行四边形（第一和第二主成分）。Harmonic GPT 倾向于生成更“矩形”的平行四边形，而标准 GPT 则生成扁平的“平行四边形”。

结论与展望

本文通过引入调和损失，为神经网络和大型语言模型提供了一种新的训练机制，显著提升了模型的可解释性和训练效率。未来的研究可以进一步探索调和损失在更大规模模型中的适用性及其在各类应用场景中的潜力，为构建更鲁棒和高效的神经网络模型铺平道路。

彭晨 | 编译

大模型2.0读书会启动

o1模型代表大语言模型融合学习与推理的新范式。集智俱乐部联合北京师范大学系统科学学院教授张江、Google DeepMind研究科学家冯熙栋、阿里巴巴强化学习研究员王维埙和中科院信工所张杰共同发起「大模型II：融合学习与推理的大模型新范式」读书会，本次读书会将关注大模型推理范式的演进、基于搜索与蒙特卡洛树的推理优化、基于强化学习的大模型优化、思维链方法与内化机制、自我改进与推理验证。希望通过读书会探索o1具体实现的技术路径，帮助我们更好的理解机器推理和人工智能的本质。

从2024年11月30日开始，预计每周六进行一次，持续时间预计 6-8 周左右。欢迎感兴趣的朋友报名参加，激发更多的思维火花！

详情请见：大模型2.0读书会：融合学习与推理的大模型新范式！

推荐阅读

1. 大语言模型会推理吗？

2. 大模型预测问题的计算复杂度，用不同能力的LLMs协作提高推理效率

3. 因果推理与大语言模型：开辟因果关系的新前沿

4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程

5. 解锁集智全站内容，开启新年学习计划

6. 加入集智，一起复杂！

点击“阅读原文”，报名读书会

内容中包含的图片若涉及版权问题，请及时与我们联系删除

调和损失的原理与优势

实验方法与结果

结论与展望

Fish AI Reader

FishAI

联系邮箱 441953276@qq.com

相关标签