文章探讨了蛋白质结构的可能性，基于20种氨基酸的排列组合，理论上存在20的100次方种蛋白质。但并非所有排列都能稳定存在，文章考察了在60秒内能保持结构的蛋白质比例，并引入了Ramachandran图，解释了氨基酸骨架角度的限制。某些形状如立方体因原子重叠而不可能稳定存在。文章还讨论了蛋白质功能与形状的关系，以及几何限制对蛋白质结构的约束，指出尽管某些形状在理论上不可能实现，但可以通过近似方法达到类似效果。最后，文章提出了对蛋白质形状和功能之间关系的思考，引发读者对蛋白质结构可能性边界的进一步思考。

🧪 理论上，基于20种氨基酸的排列组合，存在着庞大的蛋白质序列空间，高达20的100次方种，但这并不意味着所有序列都能稳定存在。

📐 Ramachandran图揭示了氨基酸骨架角度的限制，φ和ψ二面角的特定组合决定了蛋白质的二级结构，某些角度因原子碰撞而无法实现，这限制了蛋白质的形状。

🧊 立方体形状的蛋白质由于90度角的结构会导致侧链原子碰撞，从而难以稳定存在。这表明蛋白质的形状受到几何规则的限制，需要弯曲的形状来避免原子重叠。

🧬 尽管某些理论上的蛋白质形状不可能实现，但可以通过蛋白质工程技术来近似这些形状。例如，可以通过较大的蛋白质结构来接近立方体形状，或者通过其他方式来实现类似的功能。

🤔 蛋白质的功能主要由其形状决定，而形状的形成受到几何限制。因此，蛋白质功能与形状之间的关系是研究蛋白质结构和功能的重要方向。

Published on January 24, 2025 5:12 PM GMT

This is something I’ve been thinking about since my synthesizability article.

Let’s assume, given the base twenty amino acids that are naturally present in the human body, we have every possible permutation of them for up to 100 amino acids, stored in a box with pH 7.4 water and normal pressures and temperature and isolated from one another. In other words, we have on the order of 20^100 proteins available to us. This is a very large number.

What percentage of these proteins could be made?

Maybe all of them? But this is true of small molecules as well; technically all small molecules can exist, the vast majority of them would just instantly vanish/explode/dissolve upon their forced manifestation. Those molecules carry the term ‘impossible’ as well, but the more accurate term for them is just ‘unstable’. Really then, the question becomes not just whether we can string amino acids together in a particular sequence, but whether that sequence can maintain its existence as a protein for any meaningful amount of time. What’s meaningful? Let’s say 60 seconds. So, we take our bucket of proteins and wait 60 seconds.

Notably, this is a different question than the one examined in the paper Distinguishing Proteins From Arbitrary Amino Acid Sequences, which defines a ‘protein’ as anything that has a well-structured 3D shape. I don’t care about that, I want to confirm that all strings of arbitrary amino acids are possible to create.

How many proteins are left after these 60 seconds? Is the answer once again ‘all of them’?

As far as I tell, the answer is, again, yes. Nearly 100% of them will remain. There might be a minuscule subset that forms bizarre reactive loops or self-hydrolyzing sites (of which I can find little information on what consistently causes such sites), but for the overwhelming majority of those 20^100 sequences, there is no biochemical mechanism that disintegrates a protein in a matter of seconds at neutral pH and room temperature.

Well…that’s a boring answer.

But perhaps thinking of the space of all possible proteins in the same way we think of the space of all possible molecules in general is misleading. Amino acids are, by nature, largely non-reactive (with a few exceptions). The very property that makes proteins such excellent building blocks for life — their chemical stability —also means that most random sequences wouldn't pose inherent stability problems.

But what about functionality?

But what is functionality? Functionality in proteins are, by and large, determined by shape — the creation of deep binding pockets, catalytic residues in exact spatial arrangements, and molecular surfaces primed to recognize other proteins. Whereas for general molecules, functionality is largely driven by reactive chemistry — the ability to form and break bonds, participate in electron transfer, or engage in acid-base reactions.

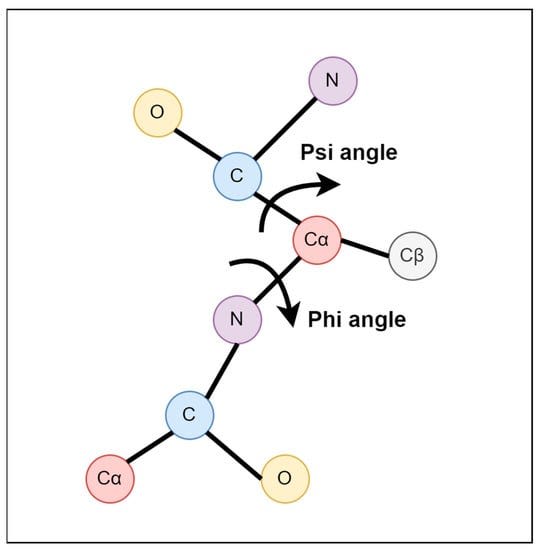
So, is there such thing as an impossible protein shape that can stably persist? To this, we can say yes. What does such an impossible shape look like? Let’s consider the Ramachandran plot. Ramachandran plots represent the backbone conformational preferences of amino acids by plotting the φ (phi) and ψ (psi) dihedral angles against each other.

What are φ and ψ dihedral angles? They represent the two primary rotatable bonds in a protein's backbone that determine its three-dimensional structure. The φ angle describes rotation around the N-Cα bond, while the ψ angle describes rotation around the Cα-C bond.

These angles are the primary determinants of a protein's secondary structure and, by extension, its overall folding pattern. As it turns out, the vast amount of angle space is simply inaccessible to amino acids. But why are some angle regions forbidden? For the simplest possible reason: it’d force atoms to nearly overlap with one another, and atoms really, really don’t like doing that.

Because of these hard geometric constraints, certain backbone configurations are physically impossible. Now, fairly, Ramachandaran Plots are constraints at the single amino-acid level, but they bubble upwards; larger secondary structures like beta-sheets and alpha-helixes still obey the fundamental rules outlined by the plot.

But I’m speaking a bit vaguely. For all I’ve said about how certain shapes are impossible, I still haven’t offered what such an impossible shape would look like.

Do we know of one?

Yes. A cube. Even part of a cube is impossible. The below picture is of a 11-residue alanine-only protein partial cube that I asked o1 to create. This shape may arise accidentally — for a few femtoseconds — from a disordered protein just fumbling around, but it is always transient and never, ever stable.

Cubes represent one of the easiest examples of a thermodynamically improbable shape due to one thing: 90 degree angles. Why? Because at the corner of such a cube, there would nearly guaranteed steric clashes (atoms that are too close) between the side chains of a given amino acid. This is why proteins have a very distinctive, curvy shape; it ensures that everything can fit together without atoms overlapping.

So, cubes are out. What else? Unfortunately, this contrived example is the best I can offer. As far I can tell, there are two grander rules about the limits of proteins structures to be observed:

If a shape demands an extremely small radius of curvature in fewer residues than physically possible, it is impossible due to the angle reasons we discussed earlier.
For example, a 3-residue ‘ring’ or the cube mentioned earlier.
If demands backbone self‐intersection or penetration through a space too narrow for the atomic radii, it is is impossible as a result of van der Waals forces.
For example, a 50‐residue chain fitting into a 3 Å diameter sphere.

It’d be difficult to use these rules to derive any meaningful number on the number of possible shapes. But we should at least be able to say that it is fewer than 100% of any given shape. There’s also a nuanced bit on conformational accessibility. Even if a shape is geometrically possible, is it always kinetically or thermodynamically accessible to a real protein? That could be a separate essay in of itself, so I’ll leave that to a future post.

Now, fairly, how meaningful is all this? Does it matter that we cannot create the protein shapes we’ve discussed here? It’s unfortunately an unknown-unknown question, which are hard to answer. Maybe extremely small radii rings would actually be quite useful for something, as would be proteins that have many residues but can be compacted into something quite small. But, at the same time, I imagine that the functionality afforded by both of these impossible shapes could very well be achieved by something that is geometrically possible.

For example, let’s say you wanted a protein that has a stable fold that looks like the letter ‘H’. You may instinctively say ‘that’s not possible!’, given the 90° degree angles in the shape. But such a shape can exist according to the Generate:Biomedicine Chroma models, which, fairly, may not turn out to fold in such a way in the real world, but you can observe that the ‘H’-ness is roughly recapitulated.

Similarly, for the protein cube we so harshly denigrated as impossible, protein engineering efforts show that you can get pretty damn close to a cube! While a cube may be nearly impossible to create using a small protein, a large enough one can get it roughly close.

So…in the end, it may turn out that while some theoretical protein shapes are impossible, you can approximate all possible shapes so well that it’s a nonexistent problem. This all said, the topic of this essay does go pretty far outside of my knowledge base. Would love to know if anyone has any thoughts on this!

Discuss