

关键词:近似纳什均衡,有限正则博弈,自动化方法

导 读
本文是 WINE 2024 入选论文 A Computer-aided Approach for Approximate Nash Equilibria 的解读。该工作由北京大学前沿计算研究中心邓小铁课题组完成。
文章给出了一个框架 LegoNE,允许人类任意编程近似纳什均衡算法,并由计算机自动计算和证明算法的近似界。利用这一人机协作的框架,文章设计了一种全新的三人博弈算法,改进了三人博弈的近似界,这是人类史上第一次对三人近似界的直接改进。
论文作者包括:邓小铁(北京大学),李东晨(香港大学),和李翰禹(北京大学)。
01
近似纳什均衡的算法挑战
纳什均衡(NE)是博弈论中最深入研究的概念之一。几十年来,NE 已经成为理论界的一块研究基石,受到了经济学、计算机、人工智能、逻辑学等领域的广泛关注,它的计算复杂性和算法问题被大量研究过。
在复杂性问题方面,过去二十年中,通过一系列里程碑的工作,我们已经发展出一套深刻的理论来揭示 NE 计算之难。在不同博弈场景下,NE 计算都被证明是很困难的,即不太可能有多项式时间算法。这些场景包括图上的博弈、多项式矩阵(polymatrix)博弈、三人博弈和二人博弈。NE 不仅精确计算是难的,对于常数近似,我们也知道它是困难的。
与 NE 的复杂性结果大为不同的是,常数近似的 NE 算法(ANE)进展非常有限。对于多人博弈,用概率方法,我们可以得到已知的唯一的准多项式时间算法。而在多项式时间范围内,进展主要集中在二人博弈,近似界的结果从
然而,这些技术有很大的局限性,无法得到有效扩展。在这些技术中,Tsaknakis 和 Spirakis 提出的梯度下降方法给这一问题的研究带来了重要的影响。梯度下降法是当前和之前最佳近似界算法设计的核心,这一方法还可以扩展到多项式矩阵博弈,这是我们唯二知道的多人博弈上的算法结果。另一个已知的多人博弈技术是扩展技术,它把一个
算法结果的停滞不前,似乎可以从下面的观察略窥一二:即便是二人博弈,近似界的改进也变得越来越困难,并且需要更长的证明。对于多人博弈,文献几乎空白。这表明,当前的算法分析可能具有内在的“证明复杂性”,已经超出了人类的能力范围。
02
LegoNE:
由机器完成 ANE 算法的近似分析
为了解决这一挑战,文章提出了一个新的框架,LegoNE 来设计和分析 ANE 算法。LegoNE 借鉴了模块化算法设计的概念:算法可以通过更小的、可重用的基本块来构建——就像使用乐高积木来搭建复杂的结构一样。
LegoNE 具有以下关键特点:
LegoNE 编程语言允许用户采用乐高风格的设计模式,为
在定义完算法后,LegoNE 框架可以读入这个算法,然后自动计算该算法的近似界,并证明其正确性。
LegoNE 非常强大,它能够复现文献中所有的二人博弈算法,计算并证明相同的近似界。对于三人博弈,在 LegoNE 的辅助下,文章作者得以在更高的视角思考问题,获得新的见解,进而提出了一种新的算法,其近似界为
03
LegoNE 的技术概要
接下来,我们以文献中经典的 DMP 算法为例,简要介绍 LegoNE 的原理。这是一个二人博弈的算法,文献已经证明,它的近似界是
首先,我们介绍一些基本符号,玩家
策略组合
接下来,我们给出 DMP 算法的基本块和 DMP 算法本身:
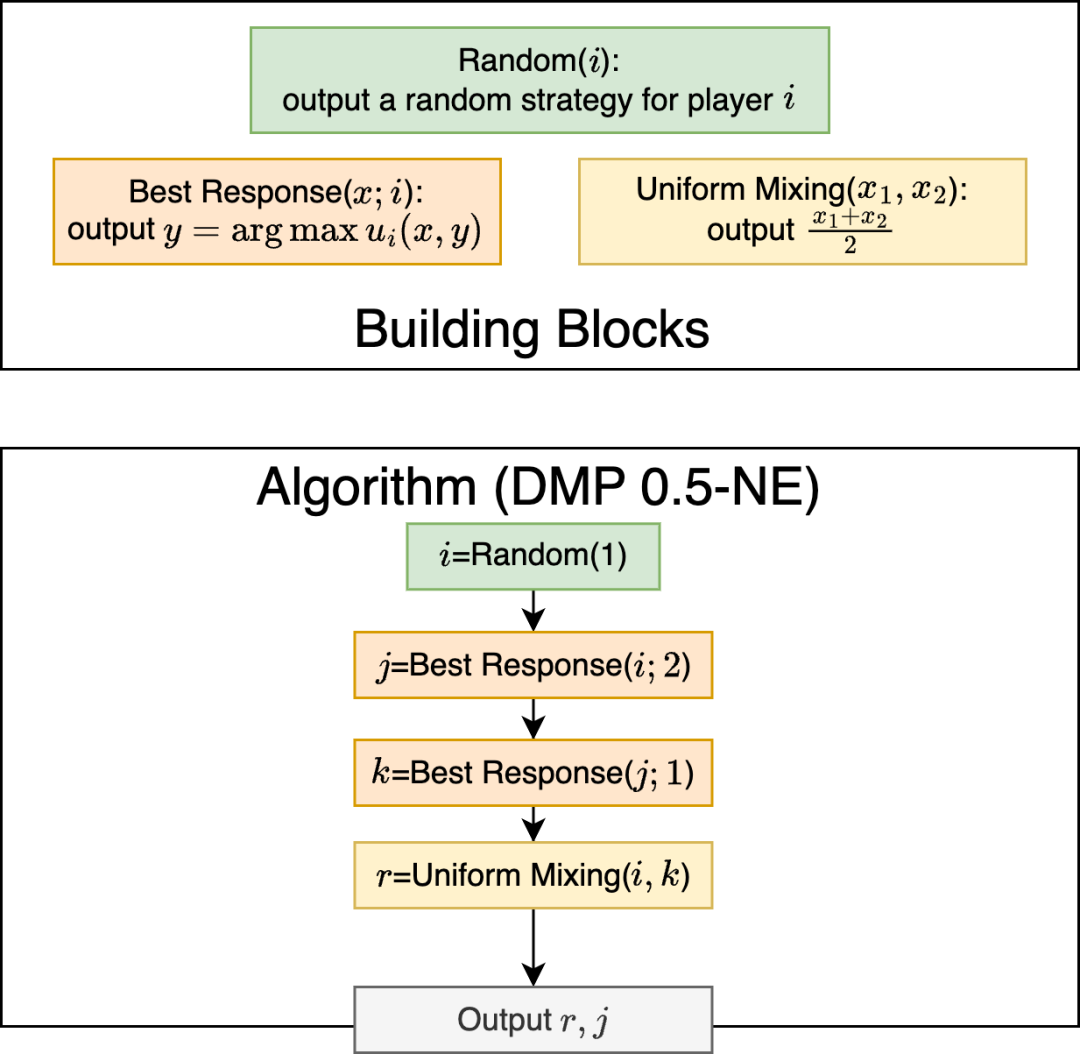
有了 DMP 算法的描述,我们现在来阐述 LegoNE 如何自动分析 DMP 算法的近似界。
首先,思考一下我们人类是如何做算法分析的。关键的一步是,我们需要知道算法的性质。这可以用逻辑公式来描述,即逻辑嵌入。例如算法第二步
最后,我们的证明目标是,对任意实例,我们都可以证明输出
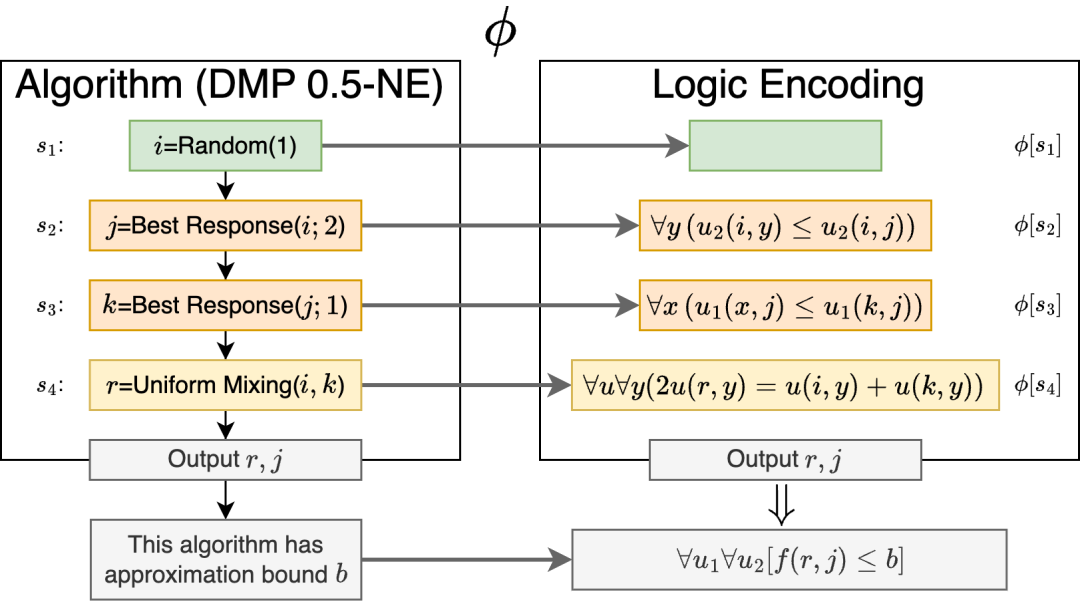
接下来,我们需要用机器证明整个逻辑嵌入是恒成立的,这是最困难的一步,我们这里只给一个粗略的思想。首先,逻辑嵌入之后,比较完整的写出来是下面的样子:
于是,对近似界的证明目标就变成了一个一阶实数算术理论的公式。这个公式的有效性(即它是否恒真)是可以用柱形代数分解算法(CAD)让计算机去判断的,于是,我们就可以自动证明 DMP 算法有
同样的方法可以用来做任何一种 LegoNE 写成的算法,特别地,我们可以用来做如下三人博弈算法。尽管这一算法非常复杂,LegoNE 依然可以顺利完成这一算法的分析,并证明它改进了近似界。

04
展望:未来在何方?
LegoNE 给出了一种算法设计与分析的新范式:人机协作。在这一范式中,人类专注于高层次的想法,负责给出算法的设计和分析中最重要的东西;而机器则负责通过预先编写好的模式进行细致且准确的分析。这样的分工让人类和机器都能够发挥各自的长处,促进更高效、更具创新性的算法开发。

图文 | 李翰禹
PKU daGAME Lab
算法博弈论实验室
Distributed and Automated Games and Managerial Economics Lab
算法博弈论实验室由邓小铁教授于2019年创立,研究方向为算法博弈论、互联网和区块链经济学、多智能体及强化深度学习理论。科研兴趣聚焦在人和智能体在互联网、物联网和区块链交互环境下多方博弈的理论与方法论建立,包括数据信息的认识论刻画、均衡和动力学分析、计算复杂性和算法设计。关注计算与通讯技术兴起中应用领域的问题,特别关注互联网广告机制设计、共享经济中的激励分析和合作竞争,以及区块链的高效共识、声誉机制和跨链机制设计。

↑↑扫码转实验室主页↑↑
实验室 PI 简介:邓小铁 讲席教授
实验室相关新闻:#PKU daGAME
daGAME近期动态


— 版权声明 —
本微信公众号所有内容,由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料,版权属北京大学前沿计算研究中心微信所有;从公开渠道收集、整理及授权转载的文字、图片和音视频资料,版权属原作者。本公众号内容原作者如不愿意在本号刊登内容,请及时通知本号,予以删除。


