🤔**贝叶斯学习视角下的神经网络：**将神经网络视为概率模型，通过贝叶斯更新（Bayes’ law）结合先验知识和数据来更新模型权重的后验分布，从而估计模型的不确定性。

🎲**蒙特卡洛采样：**由于后验分布难以直接计算，可以通过蒙特卡洛采样方法，从后验分布中抽取样本，并利用样本的平均值来近似后验分布，从而得到不确定性估计。

🤔**变分推断：**使用一个易于处理的分布来近似真实的后验分布，并通过最小化KL散度来找到最优的近似分布，从而获得不确定性估计，同时引入正则化。

💧**Dropout作为不确定性估计方法：**在训练时使用Dropout，并在推理时也使用Dropout，通过多次预测并计算预测结果的方差来获得模型的不确定性估计。

⚖️**两种方法的比较：**变分推断具有较高的偏差但较低的方差，而采样方法具有较低的偏差但较高的方差，需要根据具体情况选择合适的方案。

This is a joint post with Inbar Naor. Originally published at engineering.taboola.com.

Understanding what a model doesn’t know is important both from thepractitioner’s perspective and for the end users of many different machinelearning applications. In our previous blogpost wediscussed the different types of uncertainty. We explained how we can use it tointerpret and debug our models.

In this post we’ll discuss different ways to obtain uncertainty in Deep NeuralNetworks. Let’s start by looking at neural networks from a Bayesian perspective.

Bayesian learning 101

Bayesian statistics allow us to draw conclusions based on both evidence (data)and our prior knowledge about the world. This is often contrasted withfrequentist statistics which only consider evidence. The prior knowledgecaptures our belief on which model generated the data, or what the weights ofthat model are. We can represent this belief using a prior distribution \(p(w)\)over the model’s weights.

As we collect more data we update the prior distribution and turn in into aposterior distribution using Bayes’ law, in a process called Bayesianupdating:

\(p(w|X,Y) = \frac{p(Y|X,w) p(w)}{p(Y|X)}\)

This equation introduces another key player in Bayesian learning — thelikelihood, defined as \(p(y|x,w)\). This term represents how likely the data is,given the model’s weights \(w\).

Neural networks from a Bayesian perspective

A neural network’s goal is to estimate the likelihood \(p(y|x,w)\). This is trueeven when you’re not explicitly doing that, e.g. when you minimizeMSE.

To find the best model weights we can use Maximum Likelihood Estimation (MLE):

Alternatively, we can use our prior knowledge, represented as a priordistribution over the weights, and maximize the posterior distribution. Thisapproach is called Maximum Aposteriori Estimation (MAP):

The term \(\text{log}P(w)\), which represents our prior, acts as a regularization term.Choosing a Gaussian distribution with mean 0 as the prior, you’ll get themathematical equivalence of L2 regularization.

Now that we start thinking about neural networks as probabilistic creatures, wecan let the fun begin. For start, who says we have to output one set of weightsat the end of the training process? What if instead of learning the model’sweights, we learn a distribution over the weights? This will allow us toestimate uncertainty over the weights. So how do we do that?

Once you go Bayesian, you never go back

We start again with a prior distribution over the weights and aim at findingtheir posterior distribution. This time, instead of optimizing the network’sweights directly we’ll average over all possible weights (referred to asmarginalization).

At inference, instead of taking the single set of weights that maximized theposterior distribution (or the likelihood, if we’re working with MLE), weconsider all possible weights, weighted by their probability. This is achievedusing an integral:

\(p(y|x,X,Y) = {\displaystyle \int} p(y|x,w)p(w|X,Y)dw\)

\(x\) is a data point for which we want to infer \(y\), and \(X\),\(Y\) are trainingdata. The first term \(p(y|x,w)\) is our good old likelihood, and the second term\(p(w|X,Y)\) is the posterior probability of the model’s weights given the data.

We can think about it as an ensemble of models weighted by the probability ofeach model. Indeed this is equivalent to an ensemble of infinite number ofneural networks, with the same architecture but with different weights.

Are we there yet?

Ay, There’s the rub! Turns out that this integral is intractable in most cases.This is because the posterior probability cannot be evaluated analytically.

This problem is not unique to Bayesian Neural Networks. You would run into thisproblem in many cases of Bayesian learning, and many methods to overcome thishave been developed over the years. We can divide these methods into twofamilies: variational inference and sampling methods.

Monte Carlo sampling

We have a problem. The posterior distribution is intractable. What if instead ofcomputing the integral over the true distribution we’ll approximate it with theaverage of samples drawn from it? One way to do that is the Markov Chain MonteCarlo— you construct a markov chain with the desired distribution as its equilibriumdistribution.

Variational Inference

Another solution is to approximate the true intractable distribution with adifferent distribution from a tractable family. To measure the similarity of thetwo distribution we can use KL divergence:

\(D_{KL}(p||q) = {\displaystyle \int}_{-\infty}^{\infty} p(x) log \frac{p(x)}{q(x)}dx\)

Let \(q\) be a variational distribution parameterized by \(\theta\). We want to find thevalue of \(\theta\) that minimizes the KL divergence:

Look at what we’ve got: the first term is the KL divergence between thevariational distribution and the prior distribution. The second term is thelikelihood with regards to \(q_\theta\). So we’re looking for \(q_\theta\) that explains thedata best, but on the other hand is as close as possible to the priordistribution. This is just another way to introduce regularization into neuralnetworks!

Now that we have \(q_\theta\) we can use it to make predictions:

\(q_\theta(y|x) = {\displaystyle \int} p(y|x,w)q_\theta(w)dw\)

The above formulation comes from a work byDeepMind in 2015. Similarideas were presented bygraves in 2011 and go backto Hinton and van Camp in1993. The keynote in NIPSBayesian Deep Learning workshop had a very nice overview of how these ideasevolved over the years.

OK, but what if we don’t want to train a model from scratch? What if we have atrained model that we want to get uncertainty estimation from? Can we do that?

It turns out that if we use dropout during training, we actually can.

Professional data scientists contemplating the uncertainty of their model — anillustration

Dropout as a mean for uncertainty

Dropout is a well used practiceas a regularizer. In training time, you randomly sample nodes and drop them out,that is — set their output to 0. The motivation? You don’t want to over rely onspecific nodes, which might imply overfitting.

In 2016, Gal and Ghahramani showedthat if you apply dropout at inference time as well, you can easily get anuncertainty estimator:

Infer \(y|x\) multiple times, each time sample a different set of nodes to drop out.Average the predictions to get the final prediction \(\mathbb{E}(y|x)\).Calculate the sample variance of the predictions.

That’s it! You got an estimate of the variance! Theintuitionbehind this approach is that the training process can be thought of as training\(2^m\) different models simultaneously — where m is the number of nodes in thenetwork: each subset of nodes that is not dropped out defines a new model. Allmodels share the weights of the nodes they don’t drop out. At every batch, arandomly sampled set of these models is trained.

After training, you have in your hands an ensemble of models. If you use thisensemble at inference time as described above, you get the ensemble’suncertainty.

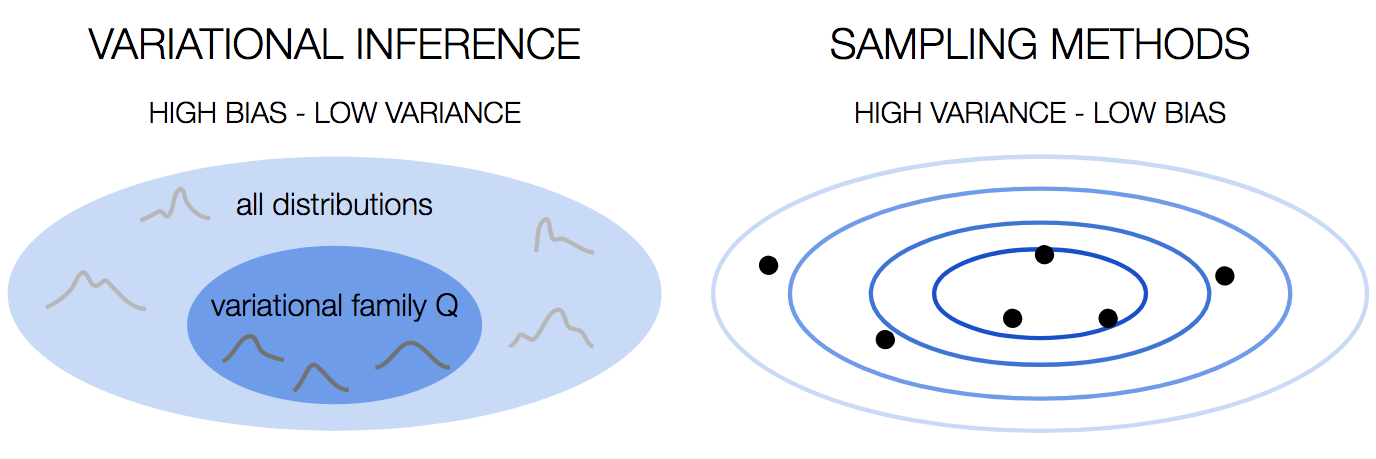
Sampling methods vs Variational Inference

In terms of the bias-variancetradeoff, variationalinference has high bias because we choose the distributions family. This is astrong assumption that we’re making, and as any strong assumption, it introducesbias. However, it’s stable, with low variance.

Sampling methods on the other hand have low bias, because we don’t makeassumptions about the distribution. This comes at the price of high variance,since the result is dependent on the samples we draw.

Final thoughts

Being able to estimate the model uncertainty is a hot topic. It’s important tobe aware of it in high risk applications such as medical assistants andself-driving cars. It’s also a valuable tool to understand which data couldbenefit the model, so we can go and get it.

In this post we covered some of the approaches to get model uncertaintyestimations. There are many more methods out there, so if you feel highlyuncertain about it, go ahead and look for more data ?

In the next post we’ll show you how to use uncertainty in recommender systems,and specifically — how to tackle the exploration-exploitationchallenge. Stay tuned.

This is the second post of a series related to a paper we’re presenting in aworkshop in this year KDD conference: deep density networks and uncertainty inrecommender systems.

The first post can be foundhere.