In the last couple of years deep learning (DL) has become a main enabler forapplications in many domains such as vision, NLP, audio, click stream data etc.Recently researchers started to successfully apply deep learning methods tograph datasets in domains like social networks, recommender systems and biology,where data is inherently structured in a graphical way.
So how do Graph Neural Networks work? Why do we need them?
The Premise of Deep Learning
In machine learning tasks involving graphical data, we usually want to describeeach node in the graph in a way that allows us to feed it into some machinelearning algorithm. Without DL, one would have to manually extract features,such as the number of neighbors a node has. But this is a laborious job.
This is where DL shines. It automatically exploits the structure of the graph inorder to extract features for each node. These features are called embeddings.
The interesting thing is, that even if you have absolutely no information aboutthe nodes, you can still use DL to extract embeddings. The structure of thegraph, that is — the connectivity patterns, hold viable information.
So how can we use the structure to extract information? Can the context of eachnode within the graph really help us?
Learning from Context
One well known algorithm that extracts information about entities using contextalone isword2vec. Theinput to word2vec is a set of sentences, and the output is an embedding for eachword. Similarly to the way text describes the context of each word via the wordssurrounding it, graphs describe the context of each node via neighbor nodes.
While in text words appear in linear order, in graphs it’s not the case. There’sno natural order between neighbor nodes. So we can’t use word2vec... Or can we?
Reduction like a Badass Mathematician
We can apply reduction from the graphical structure of our data into a linearstructure such that the information encoded in the graphical structure isn’tlost. Doing so, we’ll be able to use good old word2vec.
The key point is to perform random walks in the graph. Each walk starts at arandom node, and performs a series of steps, where each step goes to a randomneighbor. Each random walk forms a sentence that can be fed into word2vec. Thisalgorithm is called node2vec. There aremore details in the process, which you can read about in the originalpaper.
Case study
Taboola’s content recommender system gathers lots of data, some of which can berepresented in a graphical manner. Let’s inspect one type of data as a casestudy for using node2vec.
Taboola recommends articles in a widget shown in publishers’ websites:

Each article has named entities — the entities described by the title. Forexample, the item “the cutest dogs on the planet” contains the entities “dog”and “planet”. Each named entity can appear in many different items.
We can describe this relationship using a graph in the following way: each nodewill be a named entity, and there will be an edge between two nodes if the twonamed entities appear in the same item:
Now that we are able to describe our data in a graphical manner, let’s runnode2vec to see what insights we can learn out of the data. You can find theworking code here.
After learning node embeddings, we can use them as features for a downstreamtask, e.g. CTR (Click Through Rate) prediction. Although it could benefit themodel, it’ll be hard to understand the qualities learned by node2vec.
Another option would be to cluster similar embeddings together usingK-means, and color the nodesaccording to their associated cluster:

Cool! The clusters captured by node2vec seem to be homogeneous. In other words,nodes that are close to each other in the graph are also close to each other inthe embedding space. Take for instance the orange cluster — all of its namedentities are related to basketball.
You might wonder what is the benefit of using node2vec over classical graphicalalgorithms, such as community detection algorithms (e.g., the Girvan-Newmanalgorithm). Capturing the communityeach node belongs to can definitely be done using such algorithms, there’snothing wrong with it. Actually, that’s exactly feature engineering. And wealready know that DL can save you the time of carefully handcrafting suchfeatures. So why not enjoy this benefit? We should also keep in mind thatnode2vec learns high dimensional embeddings. These embeddings are much richerthan merely community belonging.
Taking Another Approach
Using node2vec in this use case might not be the first idea that comes to mind.One might suggest to simply use word2vec, where each sentence is the sequence ofnamed entities inside a single item. In this approach we don’t treat the data ashaving a graphical structure. So what’s the difference between this approach —which is valid, and node2vec?
If we think about it, each sentence we generate in the word2vec approach is awalk in the graph we’ve defined earlier. node2vec also defines walks on the samegraph. So they are the same, right? Let’s have a look at the clusters we get bythe word2vec approach:
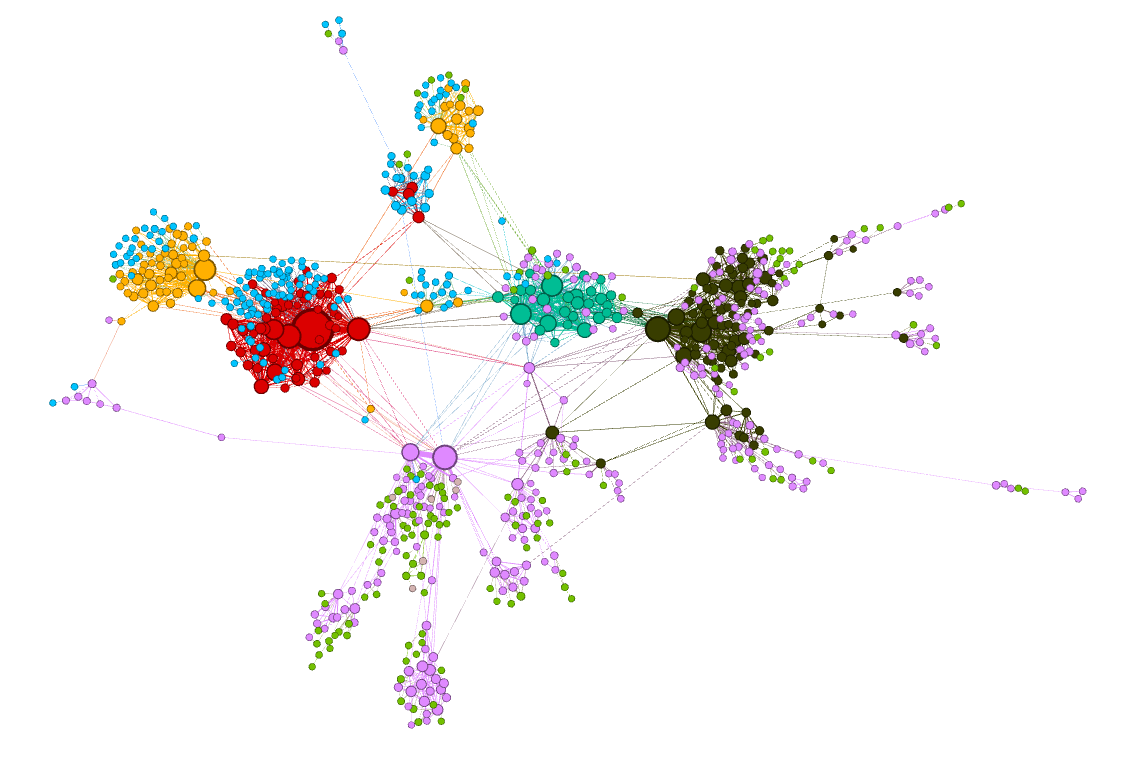
Now the “basketball” cluster is less homogenous — it contains both orange andblue nodes. The named entity “Basketball” for example was colored orange, whilethe basketball players “Lebron James” and “Kobe Bryant” were colored blue!

But why did this happen?
In this approach each walk in the graph is composed only of named entities thatappear together in a single item. It means we are limited to walks that don’t gofurther than distance 1 from the starting node. In node2vec, we don’t have thatlimit.
Since each approach uses a different kind of walks, the learnedembeddings capture a different kind of information.
To make it more concrete, consider the following example: say we have two items— one with named entities A, B, C and another with D, B, E. These items inducethe following graph:
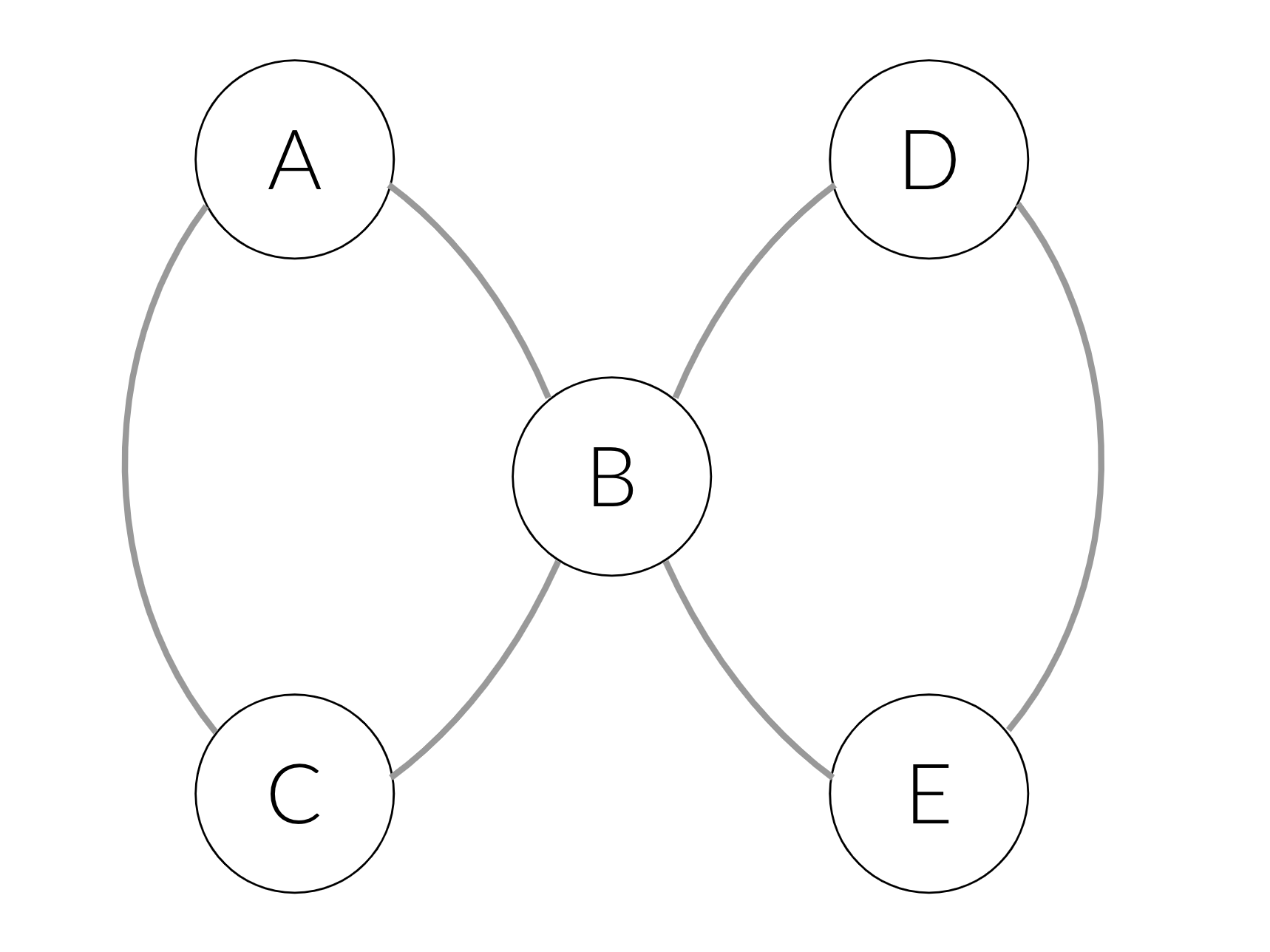
In the simple word2vec approach we’ll generate the following sentences: [A, B,C] and [D, B, E]. In the node2vec approach we could also get sentences like [A,B, E]. If we fetch the latter into the training process, we’ll learn that E andC are interchangeable: the prefix [A, B] will be able to predict both C and E.Therefore, C and E will get similar embeddings, and will be clustered together.
Takeway
Using the right data structure to represent your data is important. Each datastructure implies a different learning algorithm, or in other words — introducesa different inductive bias.
Identifying your data has a certain structure, so you can use the right tool forthe job, might be challenging.
Since so many real world datasets are naturally represented as graphs, we thinkGraph Neural Networks are a must-have in our tool box as data scientists.
Originally published atengineering.taboola.comby me and Zohar Komarovsky.

