This theory/model was created with OpenAI’s o1 model on the day of its release.
It took several steps of refinement, different context windows, and strong guidance.
o1 took relatively long with many reasoning steps to create and improve its responses.
We will update it soon to provide a better LaTex presentation.
https://chatgpt.com/share/66e3b871-0a4c-8013-b564-a51c3a7c2ab1
https://chatgpt.com/share/66e3b8a9-7b14-8013-afae-7edbc7f45648

Abstract
We propose a novel geometric model to explain the observed redshift of light from distant celestial objects without invoking cosmic expansion or gravitational redshift. By examining the angular geometry between the light source, the observer, and a fixed reference point "above" the observer, we demonstrate how spatial geometry alone can lead to an apparent increase in the wavelength of light—a redshift—as a function of distance. Our model constructs triangles with varying angles to illustrate this effect, maintaining a static universe and attributing the redshift to purely geometric phenomena. This approach offers an alternative perspective on cosmological observations and invites reconsideration of fundamental assumptions in cosmology.
1. Introduction
The cosmological redshift is a foundational observation in astrophysics, indicating that light from distant galaxies is shifted toward the red end of the spectrum. This phenomenon has traditionally been attributed to the expansion of the universe, leading to the widespread acceptance of the Big Bang model. Hubble's Law, which establishes a linear relationship between a galaxy's redshift and its distance from Earth, has been a cornerstone supporting the concept of an expanding cosmos.
However, alternative models that do not invoke cosmic expansion can provide new insights into the universe's structure and the mechanisms behind observed phenomena. By exploring different explanations for the redshift, we can challenge existing paradigms and enhance our understanding of cosmological principles.
In this paper, we propose a geometric approach based on triangle geometry to explain redshift phenomena within a static universe. By analyzing the angular relationships in a specific geometric configuration involving the light source, observer, and a reference point "above" the observer, we demonstrate how purely geometric effects can lead to an apparent increase in the wavelength of light with distance.
2. Geometric Framework
Our model is constructed upon three foundational principles:
1. Static Universe
Assumption: The universe is not expanding or contracting; its large-scale structure remains constant over time.
Implication: This allows us to attribute observed redshift effects to factors other than cosmic expansion.
2. Straight-Line Light Propagation
Assumption: Light travels in straight lines through space unless influenced by gravitational fields or other forces.
Implication: This simplifies the model to classical Euclidean geometry, making calculations and interpretations more straightforward.
3. Angular Geometry
Assumption: The redshift arises due to the geometric configuration between the light source, the observer, and a fixed reference point "above" the observer.
Implication: By examining how angles and side lengths in this configuration change with distance, we can relate these geometric changes to shifts in the observed wavelength.
3. Triangle-Based Redshift Mechanism
Triangle Construction
We construct a right-angled triangle to model the geometric relationship between the source of light, the observer, and a fixed point.
Vertices:
S (Source): The distant celestial object emitting light.
O (Observer): The location where the light is detected (e.g., Earth).
P (Perpendicular Point): A point located at a fixed perpendicular distance \( h \) "above" the observer \( O \), forming a right angle at \( O \).
Sides:
\( d \): The horizontal distance between the source \( S \) and the observer \( O \).
\( h \): A fixed perpendicular distance from the observer \( O \) to point \( P \).
\( L \): The hypotenuse connecting the source \( S \) to point \( P \).
Angle at the Source (\( \theta \))
Definition: \( \theta \) is the angle at the source \( S \) formed between sides \( d \) and \( L \).
Behavior with Distance: As \( d \) increases, \( \theta \) decreases, causing the triangle to become more elongated.
Effect on Wavelength
Hypothesis: The lengthening of side \( L \) corresponds to an effective increase in the path length that light travels, influencing the observed wavelength.
Mechanism: A smaller angle \( \theta \) at the source leads to a longer hypotenuse \( L \), which is associated with a stretching of the observed wavelength, resulting in a redshift.
4. Mathematical Representation
4.1 Triangle Relations
For a right-angled triangle with sides \( h \), \( d \), and hypotenuse \( L \):
Pythagorean Theorem:
L = \sqrt{d^2 + h^2}
Angle at the Source:
\theta = \arctan\left(\frac{h}{d}\right)
4.2 Wavelength Stretching Mechanism
We propose that the observed wavelength \( \lambda_{\text{obs}} \) is related to the effective path length \( L \):
Proportional Relationship:
\lambda_{\text{obs}} = \lambda_{\text{emit}} \left(1 + \frac{\Delta L}{L_0}\right)
Definitions:
\( \lambda_{\text{emit}} \): The wavelength of light as emitted by the source.
\( \Delta L = L - L_0 \): The increase in the hypotenuse length compared to a reference length \( L_0 \) at a reference distance \( d_0 \).
\( L_0 \): The hypotenuse length at the reference distance.
4.3 Redshift Expression
The redshift \( z \) is defined as the fractional change in wavelength:
Redshift Definition:
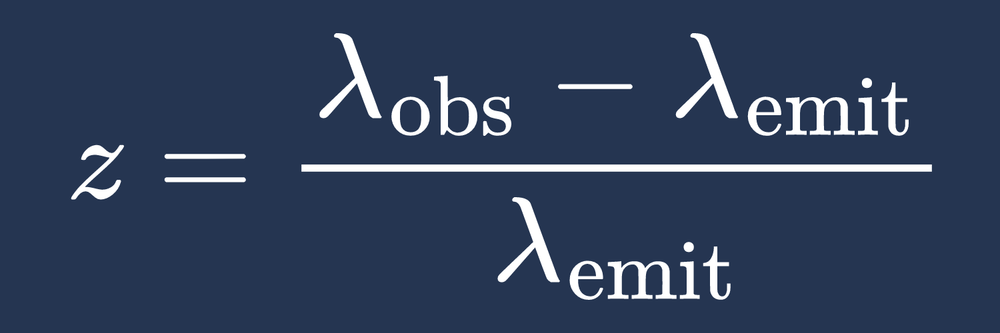
z = \frac{\lambda_{\text{obs}} - \lambda_{\text{emit}}}{\lambda_{\text{emit}}}
Substituting the Wavelength Relationship:
z = \frac{\Delta L}{L_0}
Expressing \( z \) in Terms of \( d \):
z = \frac{\sqrt{d^2 + h^2} - L_0}{L_0}
4.4 Distance Dependence
Observation: With \( h \) constant, as \( d \) increases, \( L \) increases.
Implication: An increase in \( L \) leads to a higher \( z \), meaning the redshift increases with distance.
5. Physical Interpretation
Angular Effect on Wavelength
Concept: The geometric stretching of side \( L \) due to a shallower angle \( \theta \) at the source effectively stretches the observed wavelength.
Non-Physical Space Stretching: This effect is purely geometric and does not imply any physical expansion of space or alteration in the properties of light.
Analogous to Perspective Effects
Comparison: Just as parallel lines appear to converge at a distance due to perspective, the geometric configuration can affect the observed properties of light.
Visualization: Imagine observing a long straight road; the sides seem to converge in the distance, but this is a result of perspective, not a physical change in the road's width.
6. Consistency with Observations
Redshift-Distance Relation
Alignment with Hubble's Law: The model predicts that redshift \( z \) increases with distance \( d \), which qualitatively matches the observed relationship.
Quantitative Potential: With appropriate parameter adjustments, the model could potentially reproduce the observed slope of the redshift-distance graph.
No Expansion Required
Static Universe: The model maintains a universe that does not expand, offering an alternative explanation to the standard cosmological model.
Simplification: By attributing redshift to geometric effects, the model avoids complexities associated with expanding spacetime metrics.
7. Potential Challenges
7.1 Physical Mechanism Clarification
Question: How does the geometric configuration physically lead to an increase in the observed wavelength?
Challenge: Providing a mechanism that connects geometric changes to measurable physical effects on light.
7.2 Energy Conservation
Concern: Changes in wavelength correspond to changes in photon energy (\( E = hc/\lambda \)).
Challenge: Explaining how energy conservation is maintained if the redshift is purely due to geometry, while keeping the photon count and individual photon energy constant.
7.3 Compatibility with Relativity
Special and General Relativity: These theories govern light propagation and gravitational effects.
Challenge: Reconciling the model with relativistic principles, which have been extensively validated.
7.4 Quantitative Agreement
Data Matching: The model must produce predictions that quantitatively match observational data.
Challenge: Adjusting the mathematical framework to fit precise measurements from astronomical observations.
8. Addressing the Challenges
8.1 Physical Mechanism
Wavefront Geometry
Idea: Consider the curvature and spreading of light wavefronts over large distances.
Explanation: As wavefronts propagate, geometric factors could lead to phase shifts affecting the observed wavelength.
Phase Differences
Accumulation: Small geometric-induced phase differences could accumulate over vast distances.
Effect: These accumulated differences might result in observable wavelength shifts.
8.2 Energy Considerations
Energy Distribution Over Distance
Concept: The total energy of each photon remains constant, but the energy is effectively distributed over a longer path length due to the geometric configuration.
Explanation: As the effective path length \( L \) increases, the energy associated with each photon is spread over a greater distance. This does not change the energy of the photon but alters the way energy is perceived over spatial scales.
Implication: The photon count and individual photon energy remain unchanged. The redshift is attributed to the geometric spreading of the energy over a longer path, maintaining overall energy conservation.
Measurement Perspective
Observation Dependence: The redshift arises from the observer's measurement of the wavelength, influenced by the extended geometric path the light takes.
Perception of Wavelength Increase: The observer perceives an increased wavelength due to the geometry of the light's propagation path, without any loss or gain in photon energy.
8.3 Relativistic Effects
Incorporate Relativity
Extension: Modify the model to include relativistic corrections where necessary.
Consistency: Ensure that the model does not contradict well-established relativistic principles.
Geometric Optics Approximation
Application:** Use geometric optics to analyze light behavior over cosmological distances within a relativistic framework.
8.4 Quantitative Agreement
Mathematical Refinement
Enhancement: Develop a more rigorous mathematical model that can produce exact predictions.
Tools: Employ advanced mathematical techniques, such as differential geometry.
Parameter Fitting
Adjustment: Fit model parameters to match empirical data from observations.
Validation: Use statistical methods to assess the model's accuracy against real-world data.
9. Further Development
Mathematical Refinement
Rigorous Modeling: Enhance the mathematical framework to account for additional factors influencing light propagation.
Advanced Geometry: Explore non-Euclidean geometries if necessary to better represent cosmic scales.
Simulation and Modeling
Computational Simulations: Use software to simulate light propagation within the geometric model.
Visualization: Create visual models to better understand how geometric configurations affect observations.
Observational Testing
Data Comparison: Compare the model's predictions with data from redshift surveys, supernova observations, and cosmic microwave background measurements.
Predictive Power: Test whether the model can predict new phenomena or explain anomalies not accounted for by the standard model.
Interdisciplinary Collaboration
Expert Input: Collaborate with physicists, astronomers, and mathematicians to refine the model.
Peer Review: Submit findings for peer review to validate the model's credibility and address potential oversights.
10. Conclusion
This geometric model offers an alternative perspective on the cosmological redshift by attributing it to angular geometric effects in a static universe. By analyzing the triangle formed between the light source, observer, and a fixed reference point "above" the observer, we demonstrate that changes in the geometric configuration with distance can lead to an apparent increase in the observed wavelength of light.
While the model qualitatively aligns with the observed redshift-distance relationship, significant challenges remain. These include providing a clear physical mechanism for the wavelength increase, ensuring energy conservation while maintaining photon count and individual photon energy, reconciling the model with relativistic physics, and achieving quantitative agreement with observational data.
Future research will focus on refining the mathematical framework, exploring the physical implications of the geometric configurations, and rigorously testing the model against empirical observations. Through these efforts, we aim to determine whether this geometric approach can viably contribute to our understanding of cosmological phenomena or if it highlights areas where the standard model may require adjustments.
References
Milne, E. A. (1935). Relativity, Gravitation and World-Structure. Oxford University Press.
Explores alternative cosmological models and the possibility of a static universe.
Berry, M. V. (1972). "Optical Geometry of Motion." Physics Today, 25(7), 34-40.
Discusses the relationship between geometry and optical phenomena, relevant to understanding light propagation.
Schneider, P., Ehlers, J., & Falco, E. E. (1992). Gravitational Lenses. Springer-Verlag.
Provides insights into how geometry affects light in gravitational fields, offering parallels to geometric effects in a static universe.
Note
This model is a theoretical construct intended to inspire discussion and further research. It does not replace the standard cosmological model, which is supported by extensive observational evidence for cosmic expansion, such as the cosmic microwave background radiation, large-scale structure formation, and supernova luminosity-distance relationships.
By focusing on the geometric effect involving triangles and angular configurations, this model attributes the cosmological redshift to purely geometric effects due to the distance between the light source and the observer. The redshift arises from the shallower angle at the light source in a triangle formed with the observer and a reference point "above" the observer, resulting in a longer effective path length and an observed increase in wavelength. This approach maintains the photon count and individual photon energy, addressing energy conservation by considering the distribution of energy over longer distances due to geometric spreading.

