很久以前，拜占庭帝国的一支联军包围了一座坚固的城池。为了攻下城池，各路将军需要协调一致，同时进攻才能攻破城池。但问题是，这些将军的军队分散在城池四周，互相之间仅能通过信使交流。而更大的问题则是，传闻中一些将军可能已经被敌人收买，正在密谋暗中破坏行动。

为了解决这个问题，九名将军中的主帅在一天晚上发出了召集令：“不能再拖下去了，我会在明天一早发出统一进攻或者撤退的命令，每个将军在接收到我的命令之后做决定，再将这个决定传递给其他将军，并依据收到的消息做最终判断。“同时主帅警告道：“如果我们无法确保收到的所有消息都是真实的，我们就通过多数规则来判断：若至少三分之二的将军同意进攻，就执行对应的计划，否则就撤退。”

然而，在这九名将军中，实际上有三人是叛徒。他们表面上同意主帅的方案，却秘密商议，决定在传递信息时散布混乱：

对一部分将军声称“攻城”。

对另一部分将军声称“撤退”。

偶尔自己也随意更改立场。

这种行为导致其他忠诚的将军收到的信息相互矛盾。某些忠诚的将军认为大多数人支持“攻城”，另一些则认为应该“撤退”。忠诚的将军们试图再协调，但叛徒们继续破坏，他们时而支持一方，时而支持另一方，始终让局势混乱。

当第二天结束时，忠诚的将军们发现，尽管他们都想做出正确的决定，但每个人对形势的理解完全不同。有的将军已经开始动员部队进攻，有的则在准备撤退。主帅懊恼地说道：“我们失败了！这是一个无法解决的问题！在这些叛徒存在的情况下，我们的共识永远会被打破。”

此时，远方的一位智者出现了，他解释道：“这正是分布式系统中的共识不可能性定理。在一个系统中，如果坏人的数量占总人数的三分之一或更多，他们就能通过篡改、混淆或阻断信息，永远无法让好人达成一致。这是因为在这种情况下，无论信息传播多快多可靠，坏人都可以制造矛盾。”

上述的拜占庭共识不可能性定理由 Fischer、Lynch 和 Paterson 于 1985 年提出，那么具体这个三分之一的坏人是怎么得来的呢？

我们考虑最简单的情况的数学模型，假设只有三个将军 G，A，B，其中 G 是主帅，同时三人中最多有一人是叛徒。我们用数值1代表进攻，0代表撤退，初始主帅 G 的决定为 那么拜占庭共识协议需要满足以下条件：

当 G 和 A 是好人时，G 和 A 最终都要输出。

当 G 和 B 是好人时，G 和 B 最终都要输出。

当 G 是坏人时，A 和 B 最终要输出同样的值。

假设有协议能满足这一条件，我们考虑下图的系统 S：

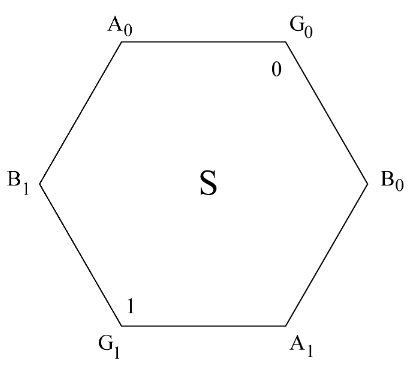
其中，六边形的每个点代表一个模拟的将军，每条边表示协议的通信，同时每个将军会根据收到的消息严格执行共识协议（即所有将军都是好人，只是通信被调整了）。例如，图中的 G₁代表初始值为1的主帅，其会给 B₁和 A₁两个将军发送消息；再例如，B₁代表一个将军，但是系统会将其计划发给将军 A 的消息都发送给 A₀（而不是给 A₁）。那么我们看看这个系统会发生什么：

因为 G₀和 A₀都是好人，所以在协议中A₀最终要输出0。

因为 G₁和 B₁都是好人，所以在协议中B₁最终要输出1。

因为 A₀和 B₁都是好人，所以在协议中 A₀和 B₁最终要输出同样的值。

以上三点产生了矛盾，说明满足条件的协议是不存在的。

对于更普遍的 n 将军情况，可以从这个简单的三将军例子归纳得到，因此在无消息认证的情况下，坏人数量在三分之一或更多时不存在共识协议能够让所有好人达成共识。

在经历了上一次叛徒破坏导致的惨败后，忠诚的将军们痛定思痛，开始思考如何确保即使存在叛徒，也能保证一致性的决策。某天夜里，将军们聚集在一个隐秘的山谷中开会，主帅说道：“如果我们不改变信息的传递方式，叛徒依然可以轻易利用伪造和篡改信息来破坏我们的共识。我们需要一种新方法，确保每条信息都能被验证是真实的。

一位年轻的将军提出了一个新方案：“我们可以引入一套加密的印章，每位将军在发出消息时，用自己的印章签名。其他将军在收到消息后，可以检查印章是否真实，并直接将带印章的消息转发出去。这种方法应该可以防止叛徒伪造信息。”主帅赞同了这个提议，并决定在即将到来的决策中试验这个“消息认证”的系统。

第二天，将军们依然面对是否全军进攻的问题。但现在，每个将军在发布自己的决策时，都会附上自己的加密签名，并通过信使将消息传递给所有其他将军。最终所有忠诚将军剔除无效消息后，基于多数规则得出统一的决策。尽管在这次会议中依然有三名叛徒试图破坏计划，但消息认证系统确保了每位忠诚将军收到的有效信息是真实的。最终，忠诚的将军成功地达成了一致的决策：全军进攻。

攻下城池后，主帅总结道：“这次成功的关键是，我们的消息认证系统让叛徒无法伪造信息。但大家要意识到，这种方法只能在叛徒数量少于一半的情况下奏效。否则忠诚者收到的大多数信息可能来自叛徒。如果我们依赖多数决策，那么叛徒依然可以操控结果。”

经过消息认证的成功试验，将军们信心倍增。然而，在下一次攻城时，他们面临一个新的挑战：这次不是攻打一座城池，而是同时围攻两座城池。每座城池依然需要所有忠诚的将军同时攻打或者撤退，否则就可能失败。然而，信心满满的主帅说到：“这个事情非常简单，明天一早我会发出两份消息，分别是针对两个城池的进攻或撤退决策，只要把上次的消息转发方式并行执行，应该就可以同时完成对两个城池的进攻共识了。”

第二天一早，主帅发出两份消息：

城池 A 的决策：主帅签署消息支持进攻；

城池 B 的决策：主帅签署消息支持撤退。消息被所有将军按协议转发，验证签名，表面上一切进展顺利。

然而，三名叛徒意识到这是他们的机会。他们利用两座城池之间的独立性制造混乱。具体来讲，由于将军之间对城池 A 和 B 的编号并不统一，他们将一些将军支持攻击城池 A 的消息，谎称为将军要攻击的是城池 B。因为签名是真实完整的，忠诚的将军们收到的消息都能通过消息认证，却在结果上彼此矛盾。由于每个将军只能根据自己收到的信息决策，他们在城池 A 和城池 B 的计划上产生了分歧：部分将军只攻打城池 A，另一部分将军只攻打城池 B。最终，两座城池的战斗都以失败告终。

主帅愤怒地拍着桌子：“为什么消息认证系统失效了？我们明明验证了每条消息的签名！”

在战败后的反思会上，智者再次站了出来，指出了问题的根源：“我们的失败不是因为消息认证无效，而是因为并行问题中，单纯的消息认证无法确保跨多个任务的一致性。这次由于叛徒可以盗用另一个共识协议里面带签名的信息，所以消息认证并没有对协议安全产生实际的效果。所以，又回到了最开始的共识不可能性定理：如果坏人的数量占总人数的三分之一或更多，就有办法让好人无法达成一致。”

拜占庭共识问题是分布式系统中的重要问题，尤其在需要应对恶意行为或故障节点的场景中显得尤为关键。这一问题不仅是分布式系统设计的理论基础，还在区块链、分布式数据库和去中心化网络等领域得到了广泛应用。本次介绍了三种共识不可能性定理：

当无消息认证时，能达成共识的要求是坏人数量占比不能大于三分之一。

当有消息认证时，能达成共识的要求是坏人数量占比不能大于二分之一。

当有消息认证，但是并行执行时，能达成共识的要求回到了坏人数量占比不能大于三分之一。

Lamport, L.; Shostak, R.; Pease, M. The Byzantine Generals Problem. ACM Transactions on Programming Languages and Systems. 1982, 4 (3): 382–401.

Dolev, D., Strong, H. R. 1983. Authenticated algorithms for byzantine agreement. SIAM J. Comput. 12, 4, 656–665.

Fischer M J, Lynch N A, Paterson M S. Impossibility of distributed consensus with one faulty process[J]. Journal of the ACM (JACM), 1985, 32(2): 374-382.

Lindell Y, Lysyanskaya A, Rabin T. On the composition of authenticated byzantine agreement[J]. Journal of the ACM (JACM), 2006, 53(6): 881-917.

文 | 李济宸