
注意:本博客于 2020 年 10 月 19 日首次发布。继 2024 年 8 月 22 日我们在《科学》杂志上发表了关于激发态的突破性研究之后,我们做了一些小更新,并在下面添加了 有关这一新阶段工作的部分。
利用深度学习解决计算量子化学的基本问题,探索物质如何与光相互作用
在《物理评论研究》上发表的一篇文章https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.2.033429中,我们展示了深度学习如何帮助解决现实世界系统中量子力学的基本方程。这不仅是一个重要的基础科学问题,而且在未来还可能带来实际用途,使研究人员能够在实验室中尝试制造新材料和化学合成之前使用计算机模拟对其进行原型设计。
我们的神经网络架构FermiNet(费米子神经网络)https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.2.033429非常适合对大量电子(化学键的基本组成部分)的量子态进行建模。我们发布了这项研究的代码https://github.com/deepmind/ferminet,以便计算物理和化学界可以借鉴我们的工作并将其应用于广泛的问题。
FermiNet 是深度学习的第一个演示,它从第一原理计算原子和分子的能量,其精度足够实用,而我们基于自我注意力的新颖架构Psiformer https://arxiv.org/abs/2211.13672仍然是迄今为止最准确的人工智能方法。
我们希望我们在人工智能(AI)研究中开发的工具和想法能够帮助解决基本的科学问题,而 FermiNet 与我们在protein folding蛋白质折叠https://deepmind.com/blog/article/AlphaFold-Using-AI-for-scientific-discovery、glassy dynamics玻璃动力学https://deepmind.com/blog/article/Towards-understanding-glasses-with-graph-neural-networks、lattice quantum chromodynamics晶格量子色动力学https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.121601和许多其他项目方面的工作一起将这一愿景变成现实。
量子力学简史
提到“量子力学”,你最有可能引发困惑。这个短语让人联想到薛定谔的猫,它既可以活着,又可以死去,还有基本粒子,它们在某种程度上也是波。
在量子系统中,电子等粒子没有像传统描述中那样的确切位置。相反,它的位置由概率云描述——它被涂抹在它允许的所有地方。这种违反直觉的情况导致理查德·费曼宣称:“如果你认为你理解量子力学,那么你根本就不懂量子力学。”
尽管这个理论看起来怪异得令人毛骨悚然,但其核心可以归结为几个简单的方程。其中最著名的方程是薛定谔方程,它描述了量子尺度上粒子的行为,就像牛顿运动定律描述了我们更熟悉的人类尺度上的物体的行为一样。虽然这个方程的解释会让人绞尽脑汁,但数学运算起来要容易得多,因此当教授们面对学生提出的棘手的哲学问题时,他们通常会告诫他们“闭嘴,好好计算”。
这些方程足以描述我们在原子和原子核层面上看到的所有熟悉物质的行为。它们的反直觉性质导致了各种奇异现象:超导体、超流体、激光和半导体都是因为量子效应才有可能出现的。但即使是不起眼的共价键——化学的基本组成部分——也是电子量子相互作用的结果。
20 世纪 20 年代,这些规则被制定出来后,科学家们首次意识到,他们首次拥有了一套有关化学如何运作的详细理论。原则上,他们可以为不同的分子建立这些方程,求解系统的能量,并找出哪些分子是稳定的,哪些反应会自发发生。但当他们坐下来真正计算这些方程的解时,他们发现他们只能精确计算最简单的原子(氢原子),而几乎无法计算其他原子。其他一切都太复杂了。
“因此,物理学和整个化学领域数学理论所必需的基本物理定律已经完全为人所知,唯一的困难是这些定律的精确应用会导致方程过于复杂而无法求解。因此,开发应用量子力学的近似实用方法成为当务之急。
保罗·狄拉克,量子力学创始人,1929 年
许多人继承了狄拉克的事业,很快物理学家们就建立了可以近似分子键和其他化学现象的定性行为的数学技术。这些方法从电子行为的近似描述开始,这种描述在入门化学中可能很常见。
在这个描述中,每个电子被分配到一个特定的轨道,这给出了在原子核附近任何一点发现单个电子的概率。每个轨道的形状取决于所有其他轨道的平均形状。由于这种“平均场”描述将每个电子视为只分配到一个轨道,因此它对电子的实际行为的描述非常不完整。尽管如此,它足以估计分子的总能量,误差仅为 0.5% 左右。
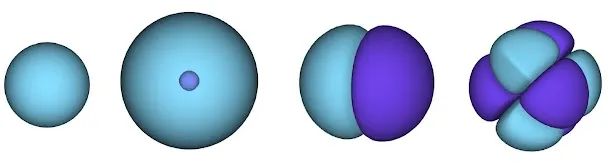
原子轨道示意图。表面表示找到电子的概率较高的区域。在蓝色区域,波函数为正,而在紫色区域,波函数为负。
不幸的是,0.5% 的误差对于化学工作者来说仍然不够。分子键中的能量只是系统总能量的一小部分,而正确预测分子是否稳定通常仅取决于系统总能量的 0.001%,或剩余“关联”能量的约 0.2%。
例如,虽然丁二烯分子中电子的总能量接近每摩尔 100,000 千卡,但分子不同可能形状之间的能量差异仅为每摩尔 1 千卡。这意味着,如果你想正确预测丁二烯的自然形状,那么需要的精度与测量足球场的宽度(精确到毫米)相同。
第二次世界大战后,随着数字计算的出现,科学家们开发了一系列超越电子平均场描述的计算方法。虽然这些方法有各种各样的缩写,但它们通常都落在了以准确性和效率为代价的轴上。一个极端是本质上精确的方法,但其扩展性会随着电子数量的增加而呈指数级下降,这使得它们不适用于除最小分子以外的所有分子。另一个极端是线性扩展的方法,但不太准确。这些计算方法对化学实践产生了巨大的影响——1998年诺贝尔化学奖授予了许多这些算法的创始人。
费米子神经网络
尽管现有的计算量子力学工具范围很广,但我们仍认为需要一种新方法来解决高效表示问题。这是因为,即使是最近似的方法,最大的量子化学计算也只能处理数万个电子,而分子动力学等经典化学计算技术可以处理数百万个原子。
经典系统的状态很容易描述——我们只需跟踪每个粒子的位置和动量。表示量子系统的状态则更具挑战性。必须为电子位置的每种可能配置分配一个概率。这被编码在波函数中,波函数为电子的每种配置分配一个正数或负数,波函数的平方给出了找到该配置的系统的可能性。
所有可能配置的空间是巨大的——如果你试图将其表示为一个每个维度有 100 个点的网格,那么硅原子可能的电子配置数量将大于宇宙中原子的数量。这正是我们认为深度神经网络可以提供帮助的地方。
过去几年,在用神经网络表示复杂高维概率分布方面取得了巨大进步。我们现在知道如何高效且可扩展地训练这些网络。我们猜测,鉴于这些网络已经证明了它们能够拟合人工智能问题中的高维函数,也许它们也可以用来表示量子波函数。
Giuseppe Carleo、Matthias Troyer 等研究人员https://science.sciencemag.org/content/355/6325/602.abstract已经展示了如何使用现代深度学习来解决理想化的量子问题。我们希望使用深度神经网络来解决化学和凝聚态物理中更现实的问题,这意味着将电子纳入我们的计算中。
处理电子时只有一个问题。电子必须遵循泡利不相容原理,这意味着它们不能同时出现在同一个空间中。这是因为电子是一种被称为费米子的粒子,其中包括大多数物质的组成部分:质子、中子、夸克、中微子等。它们的波函数必须是反对称的。如果交换两个电子的位置,波函数就会乘以 -1。这意味着如果两个电子彼此叠在一起,波函数(以及这种结构的概率)将为零。
这意味着我们必须开发一种新型神经网络,该网络相对于其输入是反对称的,我们称之为 FermiNet。在大多数量子化学方法中,反对称性是使用称为行列式的函数引入的。矩阵的行列式具有这样的特性:如果交换两行,输出将乘以 -1,就像费米子的波函数一样。
因此,你可以获取一堆单电子函数,对系统中的每个电子进行求值,然后将所有结果打包到一个矩阵中。该矩阵的行列式就是一个完全反对称的波函数。这种方法的主要限制在于,得到的函数(称为斯莱特行列式)不是很通用。
真实系统的波函数通常要复杂得多。改进此问题的典型方法是采用斯莱特行列式的大型线性组合(有时是数百万或更多),并添加一些基于电子对的简单校正。即便如此,这可能还不足以准确计算能量。
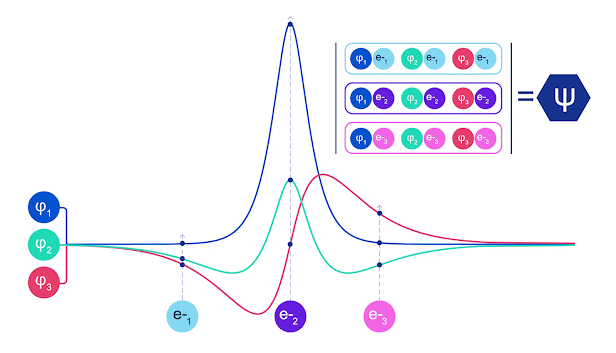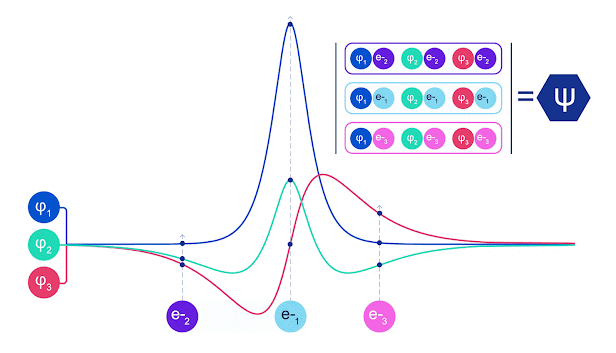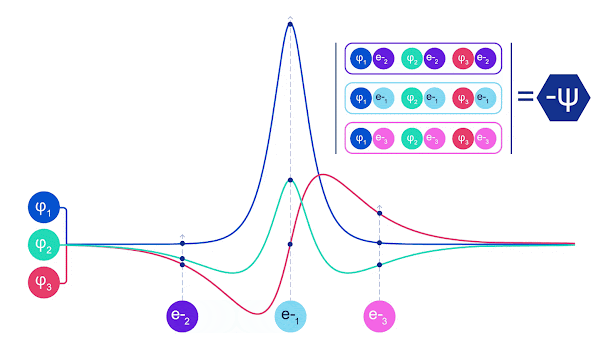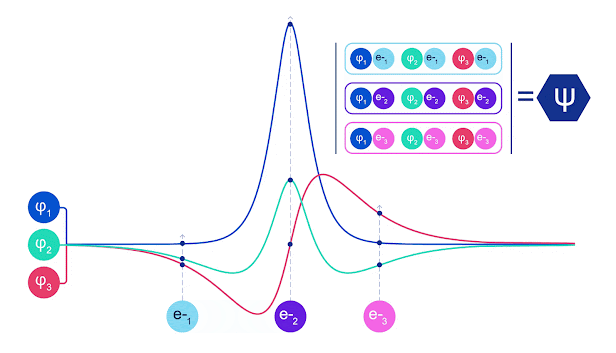
斯莱特行列式的动画。每条曲线都是上面显示的轨道之一的切片。当电子 1 和 2 交换位置时,斯莱特行列式的行会交换,波函数乘以 -1。这保证了泡利不相容原理得到遵守。
深度神经网络在表示复杂函数方面通常比基函数的线性组合更有效。在 FermiNet 中,这是通过使每个进入行列式的函数成为所有电子的函数来实现的(见脚注)。这远远超出了仅使用单电子和双电子函数的方法。FermiNet 为每个电子提供单独的信息流。如果这些流之间没有任何相互作用,网络的表现力将不会比传统的 Slater 行列式更强。
为了超越这一点,我们将网络每一层的所有流中的信息平均起来,并将这些信息传递给下一层的每个流。这样,这些流就具有正确的对称性,可以创建一个反对称函数。这类似于图神经网络https://deepmind.com/blog/article/traffic-prediction-with-advanced-graph-neural-networks在每一层聚合信息的方式。
与斯莱特行列式不同,费米网络是通用函数逼近器https://arxiv.org/abs/2007.15298,至少在神经网络层足够宽的极限下是如此。这意味着,如果我们能够正确训练这些网络,它们应该能够拟合薛定谔方程的近乎精确的解。
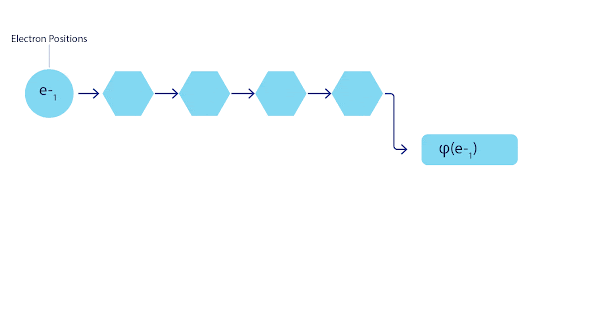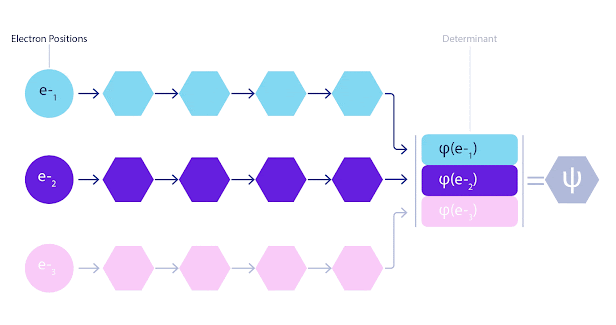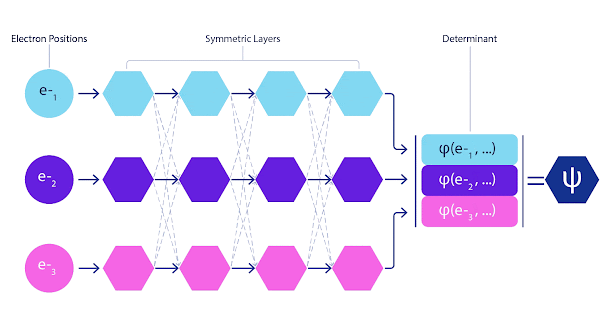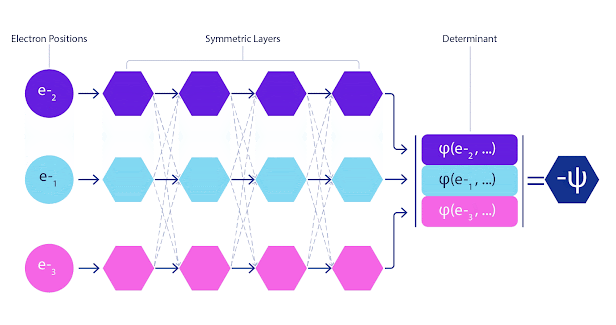
FermiNet 动画。网络中的单个流(蓝色、紫色或粉色)的功能与传统轨道非常相似。FermiNet 引入了流之间的对称相互作用,使波函数更加通用和富有表现力。就像传统的斯莱特行列式一样,交换两个电子位置仍然会导致交换行列式中的两行,并将整体波函数乘以 -1。
我们通过最小化系统能量来拟合 FermiNet。要做到这一点,我们需要评估所有可能的电子配置的波函数,所以我们必须近似地进行。我们随机选择电子配置,在每种电子排列的局部评估能量,将每种排列的贡献相加,然后最小化这个能量而不是真实能量。这被称为蒙特卡罗方法,因为它有点像赌徒一遍又一遍地掷骰子。虽然它是近似的,但如果我们需要让它更准确,我们可以随时再次掷骰子。
由于波函数的平方给出了在任意位置观察到粒子排列的概率,因此最方便的方法是使用波函数本身生成样本——本质上就是模拟观察粒子的行为。虽然大多数神经网络都是从一些外部数据进行训练的,但在我们的例子中,用于训练神经网络的输入是由神经网络本身生成的。这意味着除了电子围绕原子核运动的位置之外,我们不需要任何训练数据。
这种基本思想被称为变分量子蒙特卡罗(简称 VMC),自 20 世纪 60 年代以来就已出现,通常被认为是一种计算系统能量的廉价但不太准确的方法。通过用 FermiNet 替换基于斯莱特行列式的简单波函数,我们大大提高了这种方法在我们研究的每个系统上的准确性。
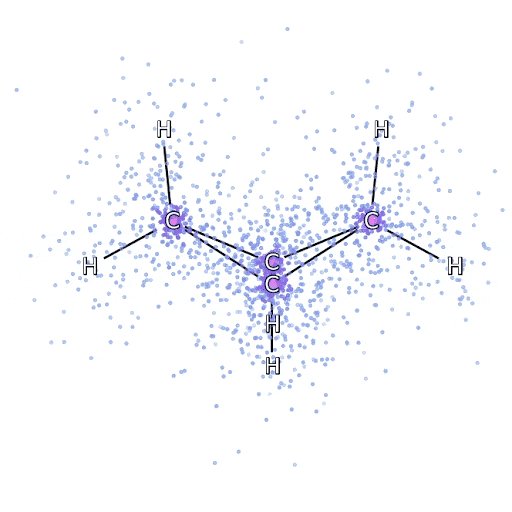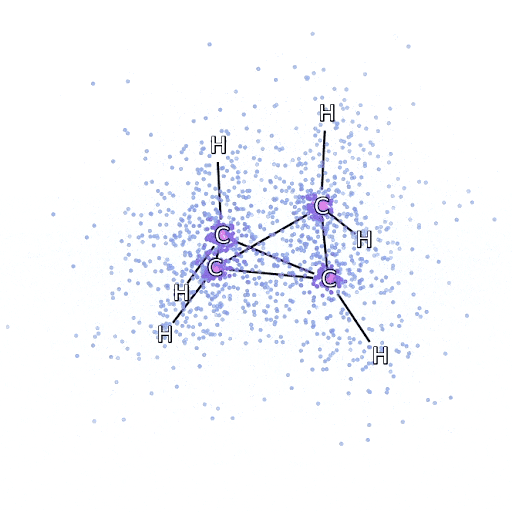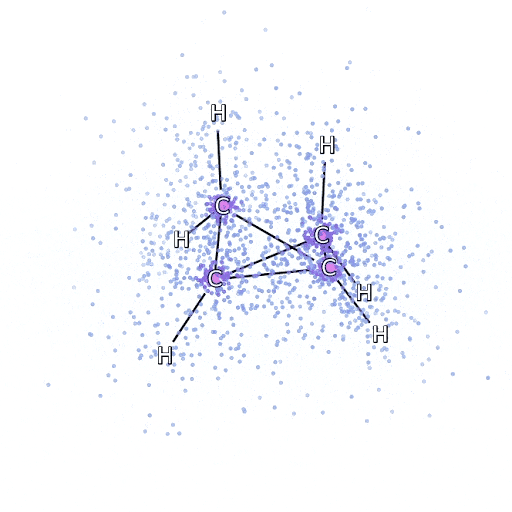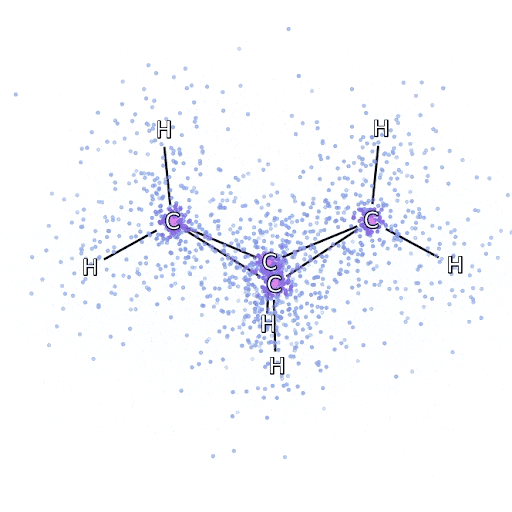
从 FermiNet 采样的模拟电子围绕双环丁烷分子移动。
为了确保 FermiNet 代表了最先进的技术,我们首先研究了简单且经过充分研究的系统,例如元素周期表第一行的原子(从氢到氖)。这些系统很小 — 10 个电子或更少 — 而且足够简单,可以用最精确(但指数级扩展)的方法来处理它们。
FermiNet 的表现远胜于同类的 VMC 计算——通常将相对于指数扩展计算的误差减少一半或更多。在较大的系统上,指数扩展方法变得难以处理,因此我们使用耦合簇方法作为基准。这种方法在分子处于稳定配置时效果很好,但当键被拉伸或断裂时就会出现问题,这对于理解化学反应至关重要。虽然它的扩展性比指数扩展好得多,但我们使用的特定耦合簇方法仍然会随着电子数量的七次方而扩展,因此它只能用于中等大小的分子。
我们将 FermiNet 应用于逐渐增大的分子,从氢化锂开始,一直到我们研究过的最大的系统双环丁烷,有 30 个电子。在最小的分子上,FermiNet 捕获了耦合簇能量与单个斯莱特行列式能量之间 99.8% 的差异,这令人震惊。在双环丁烷上,FermiNet 仍然捕获了 97% 或更多的这种关联能量,对于如此简单的方法来说,这是一个巨大的成就。
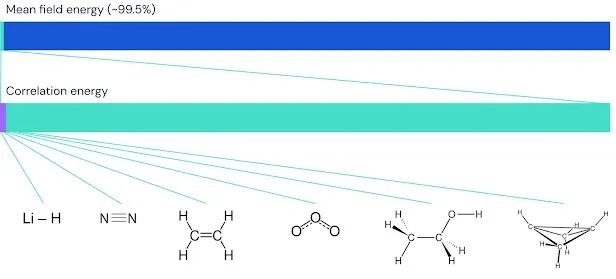
FermiNet 在分子上捕获的相关能量分数的图形描述。紫色条表示 99% 的相关能量。从左到右:氢化锂、氮、乙烯、臭氧、乙醇和双环丁烷。
虽然耦合聚类方法对稳定分子很有效,但计算化学的真正前沿是了解分子如何拉伸、扭曲和断裂。在这方面,耦合聚类方法往往很吃力,所以我们必须与尽可能多的基线进行比较,以确保得到一致的答案。
我们研究了两个基准拉伸系统:氮分子 (N2) 和具有 10 个原子的氢链 (H10)。氮是一种特别具有挑战性的分子键,因为每个氮原子贡献三个电子。与此同时,氢链对于了解电子在材料中的行为方式https://www.simonsfoundation.org/2020/09/14/infinitely-long-chains-of-hydrogen-atoms-have-surprising-properties-including-a-metallic-phase/很有价值,例如,预测材料是否导电。
在这两个系统中,耦合簇方法在平衡状态下表现良好,但在键被拉伸时会出现问题。传统的 VMC 计算在各方面表现不佳,但 FermiNet 是研究的最佳方法之一,无论键长如何。
计算激发态的新方法
2024 年 8 月,我们在《科学》杂志上发表了这项工作的下一阶段成果https://www.science.org/doi/abs/10.1126/science.adn0137。我们的研究为计算量子化学中最困难的挑战之一提出了解决方案:了解分子在受到刺激时如何从激发态转变为激发态。
FermiNet 最初专注于分子的基态,即给定一组原子核周围电子的最低能量配置。但是,当分子和材料受到大量能量的刺激(例如暴露于光或高温)时,电子可能会进入更高的能量配置,即激发态。
激发态是理解物质如何与光相互作用的基础。吸收和释放的确切能量量为不同的分子和材料创造了独特的指纹,这影响了从太阳能电池板和 LED 到半导体、光催化剂等技术的性能。它们还在涉及光的生物过程中发挥关键作用,如光合作用和视觉。
准确计算激发态的能量比计算基态能量要困难得多。即使是基态化学的黄金标准方法(如耦合簇)也显示出激发态的误差https://pubs.acs.org/doi/10.1021/acs.jctc.4c00410大了几十倍。虽然我们想将 FermiNet 的工作扩展到激发态,但现有方法的效果还不足以使神经网络与最先进的方法相媲美。
我们开发了一种计算激发态的新方法,这种方法比以前的方法更稳健、更通用。我们的方法可以应用于任何类型的数学模型,包括 FermiNet 和其他神经网络。它的工作原理是找到带有额外粒子的扩展系统的基态,因此只需稍加修改即可使用现有的优化算法。
我们在一系列基准上验证了这项工作,并获得了非常有希望的结果https://www.science.org/doi/abs/10.1126/science.adn0137。在一种名为碳二聚体的小而复杂的分子上,我们实现了 4 meV 的平均绝对误差 (MAE),这比之前的黄金标准方法 (达到 20 meV) 更接近实验结果五倍。我们还在计算化学中一些最具挑战性的系统上测试了我们的方法,其中两个电子同时被激发,结果发现我们与迄今为止最苛刻、最复杂的计算相差约 0.1 eV。
今天,我们开放我们的最新研究成果https://zenodo.org/records/11937084,并希望研究界能够以我们的方法为基础探索物质与光相互作用的意想不到的方式。
致谢
我们关于激发态的新研究是由 Ingrid von Glehn、Halvard Sutterud 和 Simon Axelrod 与大家共同开展的。
FermiNet 由 David Pfau、James S. Spencer、Alexander GDG Matthews 和 WMC Foulkes 开发。
感谢 Jess Valdez 和 Arielle Bier 对博客的支持,以及 Jim Kynvin、Adam Cain 和 Dominic Barlow 提供的数据。
脚注
FermiNet 还为每对电子提供流,这些流中的信息会传回单电子流。为简单起见,我们选择不在博客文章中对此进行可视化,但您可以在论文中找到详细信息。
参考
Pfau, D., Axelrod, S., Sutterud, H., von Glehn, I., & Spencer, J. S. (2024). Accurate computation of quantum excited states with neural networks. Science, 385(6711), eadn0137.
Pfau, D., Spencer, J. S., Matthews, A. G., & Foulkes, W. M. C. (2020). Ab initio solution of the many-electron Schrödinger equation with deep neural networks. Physical review research, 2(3), 033429.
https://github.com/google-deepmind/ferminet




