文章探讨了光在介质中动量的问题，涉及亚伯拉罕和闵可夫斯基的不同观点及争议，还通过类比、理论和实验进行分析，如跑步者类比、海森堡不确定性原理等，以及不同情况下对光动量的理解和应用。

光在介质中的动量问题复杂，如在玻璃中，若玻璃折射率为n，光在其中的速度为真空光速的1/n，但光在玻璃中的动量相对真空时的情况存在争议。亚伯拉罕认为光的动量会因介质而减少n倍，闵可夫斯基则认为会增加n倍。

以跑步者在水中的情况作类比，跑步者在水中速度减慢，其动量不能仅按速度变化简单计算，还需考虑其推动的水的动量，这与光在玻璃中涉及电磁场及物质响应的动量问题有相似性。

人们在考虑光的动量时会涉及不同情境，如理想实验中的反冲问题，以及海森堡不确定性原理。亚伯拉罕动量似乎更适用于牛顿定律，闵可夫斯基动量则与海森堡原理相关。

在材料中，电磁场的相速度和群速度不一定相等，它们暗示了两个折射率np和ng，文章提到在亚伯拉罕形式中用ng计算动动量，在闵可夫斯基形式中用np计算与不确定性原理相关的动量。

Published on October 9, 2024 8:19 PM GMT

I think that most people underestimate how many scientific mysteries remain, even on questions that sound basic.

My favourite candidate for "the most basic thing that is still unknown" is the momentum carried by light, when it is in a medium (for example, a flash of light in glass or water). 

If a block of glass has a refractive index of $n$, then the light inside that block travels $n$ times slower than the light would in vacuum. But what is the momentum of that light wave in the glass relative to the momentum it would have in vacuum?"

In 1908 Abraham proposed that the light's momentum would be reduced by a factor of $n$. This makes sense on the surface, $n$ times slower means $n$ times less momentum. This gives a single photon a momentum of $\hslash \omega /nc$. For $\omega$ the angular frequency, $c$ the speed of light and $\hslash$ the reduced Planck constant.

In 1909 Minkowski proposed that actually, the momentum of the same energy worth of light in a material is increased by a factor of n relative to vacuum. This gives a single photon momentum of $\hslash \omega n/c$.

Which was right? It's still not settled. Not really. A lot of papers will tell you that the "Abraham Minkowski Controversy" is now resolved, but they won't all agree on how it has been resolved. At least three mutually incompatible resolutions have been published. New papers claiming a resolution, or else knocking holes in the old resolutions, are still coming out.

In the rest of this post am going to sketch out why this is a complicated problem, and how some of the proposed solutions work.

 

An Analogy: The Runner

Why is the momentum of light in glass complicated?

Consider a runner running (as is usual) on land, with some speed $c$. On their route the runner encounters a region of knee-high water. While travelling through the water our runner travels at a reduced speed of $c/n$. Now, we ask, what is the momentum of the runner while they are moving through the water?

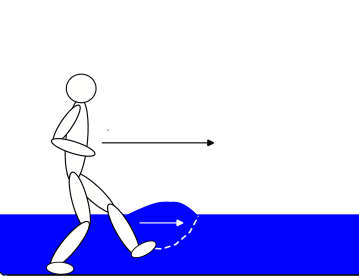
If we take the mass of everything inside the runner's skin, and multiply it by their velocity then clearly this has fallen by a factor of $n$ relative to their momentum outside the water. However, as the runner wades they will kick a parcel of water along in front of their knees. The total momentum associated with the fact that the runner is in motion is not entirely contained inside their skin.

Suppose that we place an obstacle in the runner's path. They collide with it and come to a complete stop. During the collision we record the impulse on our obstacle and infer the runner's momentum. Clearly, in the process of stopping the runner, we have also stopped the water that they were kicking along with them, so that the momentum such an experiment would detect is not simply $c/n$, but some higher value, including the water parcel. Indeed, it is not possible to run through water without pushing the water around, so whenever we compare the situation of the runner to the counter-factual where they are standing still, we need to include the momentum of that pushed water. The collision experiment is comparing exactly those states.

What if we posited imaginary "ghost water" that phased through the runner? Then we could avoid thinking about the momentum of the water and keep things simple. Yes, we could. But the ghost water also wouldn't slow the runner down, so that is just the same as the runner on land example.

In the context of the photon in glass we have the momentum in the electric and magnetic fields (like the momentum inside the runner's skin). A photon in glass "plucks" the electron orbitals of the atoms as it passes them by, depositing some amount of energy and momentum into the matter that then springs back out into the electric field a moment later. That momentary retention is the cause of the light slowing down in the first place (or at least, the momentary retention in the time domain Fourier Transforms into the frequency domain as the slow-down).

So, is it just as simple as "The Abraham momentum ($/n$) describes the electromagnetic field exclusively, while the Minkowski momentum ($\times n$) also includes the part "in the water?"" - That is one position.^[1] But alternative theories exist. A similar, competing theory claims claims that Abraham's momentum is the momentum fully in electromagnetic fields, and that some other expression [$1/2\times (n+1/n)$  - the direct average of Minkowski and Abraham] gives the total momentum including that in the material response ^[2].

 

What is momentum anyway?

I first encountered the Abraham-Minkowski controversy when I was trying to answer a question about recoil. I was considering an idealised thought experiment  ^[3] and to know if it would work I needed to know how recoil worked as light changes medium. When light goes into or out of some piece of glass, which way does the glass get shoved by the recoil, and by how much? This is a basic Newtonian problem, but to answer it one needs to know what to use for the momentum of the light when it is in glass.

Another context in which people worry about momentum is the Heisenberg Uncertainty Principle. You can't know the location and momentum of a photon at the same time, and the more you know one, the less you can know the other.

The Abraham momentum "feels more like" its trying to work with Newton, while Minkowski is Heisenberg's friend. This is basically the short version of the paper by Stephen Barnet^[4], where it is argued that the Abraham momentum is the answer to the question "What do I put in Newton's second law to calculate recoil?" and the Minkowski one answers the question "I am doing Heisenberg Uncertainty for a photon in glass, what do I use?"

While I am not convinced by the argument, I think it is getting one thing importantly right, and that is that it asks people to think about what they want to use the number (or vector) they are calculating for. A question of the type "What is X" becomes increasingly difficult to answer as more and more emphasis is put on the "is".

"What is the momentum?"
"What is the momentum?"
"What is the momentum?"
"What is the momentum?"

By asking what we want the number for we sidestep that particular rhetorical spiral, and keep ourselves arguing about physics, not definitions. ["Momentum" as a term is arguably over-loaded with too many definitions ^[5].]
 

Group Velocity vs Phase Velocity

In a material the phase velocity (how quickly the phase-fronts of the electromagnetic field propagate) and group velocity (how quickly the energy of the field propagates) are not necessarily equal, and these two velocities imply two refractive indices, $n_p$ and $n_g$ which are the slowdown factors of the two relative to vacuum. That same paper from the last section tells you to use $n_g$ in Abraham's form (dividing) for kinetic momentum and $n_p$ in Minkowski's (multiplying) for the momentum that goes with the uncertainty principle. 

 

A Clean-Cut Proof of Abraham's Result

There is a nice, simple, way of motivating that Abraham should be right. Get a glass block, throw a photon at it (from the left). For simplicity assume that the photon transmits through the block without reflection at either edge (this can be achieved using either anti-reflection coatings or post-selecting on a photon that transmits). We will also assume the glass block is rigid, so that it can be moved but doesn't support any vibrational modes (no wobbling like jelly). We also assume the glass block is on a frictionless table so is able to slide either left or right.

As the photon enters the glass block either its momentum falls (Abraham), or increases (Minkwoski). If the photon momentum falls then the glass block starts sliding left to right by momentum conservation. If instead, the momentum increases the glass block starts sliding right to left. In either case, the photon will soon exit the block from the other side and return the block to a standstill. In total the glass will have either shifted slightly left or right depending on which momentum equation is correct.

Usually in physics, for an isolated system, the centre of mass moves at a constant rate. The photon and glass block together constitute an isolated system, and energy-mass equivalence can be used to give the photon a contribution to the centre of mass. The general principle that the centre of mass moved a constant rate can only be satisfied by the glass block moving left to right, and only by it moving by exactly the distance predicted by the Abraham momentum.

Going back to our runner example, the slight shift of the block from left to right can be thought of as the splash as the runner leaves the water.

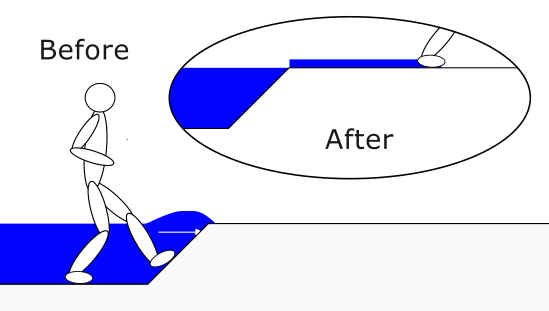
Putting the water centre of mass slightly to the right. (Although this may be taking the analogy too far). In contrast, Minkowski's momentum would have us believe the glass block gets moved in the opposite direction (towards the light source). So it is not only failing to quantitively satisfy the principle that centre of mass transport should be conserved in an isolated system, but is making a qualitatively opposite prediction, that the glass moves in the opposite direction. Note however, that the principle being broken (uniform motion of centre of mass) is not at all one of the "big principles" of physics, especially not with the extra step of converting the photon energy to mass. I had not previously heard of the principle, and don't think it is anywhere near the weight class of things like momentum conservation.

A variation on this experiment has been done. An optic fibre has a high-power flash of laser light exit from the end facet. As the laser flash leaves the glass (into air) its momentum increases (according to Abraham), which requires a reaction force against the fibre itself, propelling it backwards. So that when the light leaves the fibre springs back (video: https://journals.aps.org/prl/supplemental/10.1103/PhysRevLett.101.243601/Mvi_0025.avi). The spring-back is evidence of the Abraham version of the momentum.

One problem with this experiment is that light (by any definition) has very little momentum, so they had to put fairly high powers through a very small fibre. This means that other things (thermal expansion, static electricity etc) are pushing on the fibre as well, and we need to put some trust in estimates of how strong these competing effects are relative to the direct change in the light momentum. Also, if Minkowski was right the fibre would get tugged down, which (given some elasticity in the fibre) might look somewhat similar to it springing-back.

 

A Clean-Cut Proof of Minkowski's Result

There is a nice, simple, way of showing that Minkowski's result must be right. Get a mirror, put it in a liquid. Bounce a beam of light off the mirror, and measure the radiation pressure on said mirror as the light bounces off. Repeat for liquids of different refractive indices. Do the experiment, see that the force on the mirror increases with refractive index, as predicted by Minkowski  ^[1]. Simple, and without the measurement uncertainties of the fibre experiment.

No, too simple. While the measurement uncertainties are very low in these experiments, there is a sub-controversy about how they are to be interpreted. Mirrors are characterised not just by the fraction of the optical energy that reflects back from them, but also by the phase-shift imposed on the reflected light wave. For a metal mirror its usually a $\approx \pi$ phase shift, but any phase shift it possible with the right mirror. The contention is that the phase shift imposed by the mirror will effect the radiation pressure observed, and that all the studies to date saw the Minkowski result only because they all used mirrors with the phase shift $\pi$ ^[6]. This paper claims that to get the real momentum you need to average over mirrors with different phase shifts. My own (possibly erroneous) read on this position is that we can imagine the photon is more like a swimmer or rowing boat than a runner, and that momentum is periodically exchanged between the medium and the boat at the optical frequency. The phase on reflection from the mirror (somehow) picks out at which point in the stroke cycle we interrupt and reflect the photon, and that at different points in the cycle different amounts of momentum are in the photon itself or the medium. The claim that one should average over different mirrors leads to the claim that the correct momentum is in fact the direct average of Abraham and Minkowksi.

(Other "pro-Minkwowski" experiments exist. For example by photons being absorbed by atoms in fluid).

 

Consensus

Consensus is a poor substitute for truth. But if you are interested in the more sociological aspects of science you may well be wondering which theory is "mainstream" and which is the one beloved by cranks and crackpots. My own impression is that engaging with the discussion at all (to advocate any position) is considered slightly cranky. I can't offer evidence for this claim, its all vibes. But it remains my impression. I think its because doing the sort of physics Einstein famously did (looking to replace foundational theories) is perceived partly as a status claim, so when someone comes up with a weird new theory to replace General Relativity it is not enough to label them "wrong" (assuming they are), but the extra label "crank" is appended. Taking any stance on Abraham-Minkowski lands you squarely in the foundational theory work. If I am right about this we have something wrong with our science culture, where people are pushed away from the places of genuine disagreement, which by any reasonable standard are the places most in need of study.

 

To summarise our options:

Abraham does Newton's momentum, Minkowski Heisenberg's, (with the caveat that we use the group index for Newton and the phase index for Heisenberg).^[4]Abraham does the purely electromagnetic component of the momentum, Minkowski also includes the material contribution ^[1].Abraham does the purely electromagnetic component of the momentum. But the multiplier for the momentum including material contributions is a different expression altogether: $1/2\times (n+1/n)$. Minkowski is just wrong ^[2].Its a matter of convention how to partition the momentum between the light and the background matter in which it propagates, and any division (however arbitrary) is equally acceptable, including the Abraham and Minksowski equations ^[7]. (What stance should be taken on the value of the total momentum, and which direction the glass block is expected to move is unclear.)Abraham was just right 100 years ago, why are we still debating this?Minkowski was just right 100 years ago, why are we still debating this? (Depending on who you ask they might also tell you for good measure that Abraham was a complete hack who never got anything right in his whole career and certainly not this ^[8].)The momentum is actually given by some totally different expression.

 

My Opinion

For my own position, I want any answer to the problem to offer me the tools needed to answer my original question about weird photon-rockets ^[3], and any "resolution" that fails to offer an answer to questions of that type isn't really a resolution at all.

At the moment, if I had to pick, I would take either option (3) or possibly (2). The mirrors-in-fluid experiments appear to falsify (1), (3), (5) and (7). [Although the proponents of (3) believe that we need to repeat these experiments with a range of mirrors with different reflection phases.] (4) is unfalsifiable, makes no predictions, and therefore worse than wrong. (6) is slain by the fibre experiment, and fails to engage with the fact that there surely is some distinction between the momentum in the EM field and in the full propagating wave. I have a vague sense that having separate momenta for kinetic and uncertainty related things as in (1) breaks something important somewhere. (Perhaps it allows some scheme to beat Heisenberg uncertainty on a particle's momentum by bouncing a photon in glass of it somehow.)

An important point against theory (2) is that, despite being the most obvious resolution, it was proposed most recently (2017), which strongly implies that the first few times anyone had the idea they thought there was something wrong with it. For example, despite looking like a modified version of (2) proposal (3) actually predates it by 13 years (2004)  ^[2]. It's also unfortunate that the paper advocating most strongly for proposal (2)  ^[1], is, in my opinion, using a model at wildly the wrong level of detail. For a disagreement on a fundamental issue like this you want simple, cartoon models (frictionless, spherical cows in a perfect vacuum). If some contingent detail (the fuzziness of the cows) is changing the answer, then the answer isn't getting to the root of the disagreement. So a minimum of fuzz is good. Mikko Partanen doesn't agree with my philosophy on this and they have a kitchen-sink theory overflowing with, possibly extraneous, detail. Pushing me more towards (3) are two recent (2023) papers that both have supporting evidence for it ^[9].

 

Final Thoughts

From the list of options above I have actually left out what appears to be a fairly common position. I have left it out because it is poisonous, and unhealthy. This position goes something like: "This was never a real issue, only mad people think it ever was. Don't worry, we physicists know what we are doing, nothing to see here!" You will not find this in a paper of course, but I see variations of this position in my google searches, and have heard it expressed in person.

There are many reasons this position is poisonous. First, it seems to take a stance against asking questions, and perhaps curiosity itself. Second, it fails to actually provide the answer. Which way do these people think the glass block slides as light propagates through it? Finally, it is simply false. People have disagreed on this issue, and continue to disagree. A disagreement in physics does not mean that we have a tribe of rabid insane "cranks" fighting an enlightened group of intelligent and respectable physicists. One day this issue will be resolved, most likely one of the proposals in front of us at the moment will prove to be the answer, or most of the answer. That will not make the people who studied this problem, on any side, retrospectively insane, bad physicists or unworthy of respect. There is something to see here, a genuine disagreement on something fundamental about how light works, and I think that is exciting, and worthy of curiosity.

 

 

1. ^{^}

   "Photon mass drag and the momentum of light in a medium"
   Mikko Partanen, Teppo Häyrynen, Jani Oksanen, and Jukka Tulkki
   Phys. Rev. A 95, 063850 https://journals.aps.org/pra/abstract/10.1103/PhysRevA.95.063850 

2. ^{^}

   "Radiation pressure and the linear momentum of the electromagnetic field".
   Masud Mansuripur, Optics Express 5376, (2004) https://opg.optica.org/oe/abstract.cfm?URI=OPEX-12-22-5375 . "Resolution of the Abraham-Minkowski Controversy", Masud Mansuripur, Optics Communications, 283, 1997-2005 (2010). https://wp.optics.arizona.edu/masud/wp-content/uploads/sites/32/2019/04/Resolution-of-Abraham-Minkowski-controversy.pdf 

3. ^{^}

   Specifically, some materials have (at some frequencies) a negative index of refraction. In these materials the light's momentum (for some value of momentum) points the opposite direction to that the light propagates. I was interested in whether it was hypothetically possible to use this to build an "Internal Reaction Drive". This would consist of a loop of transparent materials that is half made of negative refractive index materials, and half normal (positive index) materials. As photons travel around the loop in circles their momenta are always in the same direction. To boost my space-ship I fire my laser to inject extra photons into the loop, and the recoil accelerates my ship. The photons are the exhaust particles, but they never leave the ship. When I reach Alpha Centauri I can start harvesting the photons back out of my loop, which will slow the ship down and eventually bring me back to a standstill. To an external observer who couldn't see the inside workings it would look like a reactionless drive. To answer my original question, which was if this Internal Reaction Drive was in principle possible, you would need a definitive answer to the question "What is the momentum of light in matter?" (For use in Newtonian recoil calculations).

   

   This is a sketch of the idea. The photons (yellow kites) go in circles, with propagation direction shown by the kite points. Their momenta (green allows) are in the same direction for most of the loop, so that the total resultant momentum increases as more photons are added. My current weakly held position is that despite appearing mad I think this might in-principle actually work, based mostly off the way momentum conservation of Cherenkov radiation in negative index materials works^[10]. Note that, if Minkowski is "just right" then you don't even need negative refractive index materials. You just make the backward part of the loop a higher index material than the forward part. This way the photons have more momentum while going backwards, and also, averaging over time, spend more time travelling backwards that forwards. In contrast, Abraham (with positive index materials) doesn't allow this as the photons spend less time going in the direction in which they have more momentum, so the time average momentum of each as it loops comes to zero. As I find the proposal itself intrinsically somewhat implausible (it is a maximally aggressive violation of the uniform motion of the centre of mass of an isolated system), I think the fact Abraham is somewhat opposed to it working is a weak update in favour of something Abraham-like.

4. ^{^}

   "Resolution of the Abraham-Minkowski Dilemma", Stephen M. Barnett, Phys. Rev. Lett. 104, 070401. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.104.070401 

5. ^{^}

6. ^{^}

   "Radiation Pressure on Submerged Mirrors: Implications for the Momentum of Light in Dielectric Media", Masud Mansuripur.  https://opg.optica.org/oe/fulltext.cfm?uri=oe-15-5-2677&id=130623 

7. ^{^}

   "Momentum of an electromagnetic wave in dielectric media" Robert N. C. Pfeifer, Timo A. Nieminen, Norman R. Heckenberg, and Halina Rubinsztein-Dunlop. Rev. Mod. Phys. 79, 1197 https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.79.1197 

8. ^{^}

   Ad hominem attacks on people 100 years dead on stack exchange! Photons have no electromagnetic charge, but are emotionally charged particles. https://physics.stackexchange.com/questions/3189/is-the-abraham-minkowski-controversy-resolved [Note the author of that answer seems to have got into enough arguments to have a RationalWiki page, which is not a thing I would wish on anybody.]

9. ^{^}

   "Revealing light momentum in dielectric media through standing-wave radiation pressure", Gopal Verma, Vinod Kumar, and Wei Li. Phys. Rev. A 108, 043514 https://journals.aps.org/pra/abstract/10.1103/PhysRevA.108.043514 . Also see  "Recoil momentum of an atom absorbing light in a gaseous medium and the Abraham-Minkowski debate", João G. L. Condé and Pablo L. Saldanha. Phys. Rev. A 108, 013511 https://journals.aps.org/pra/abstract/10.1103/PhysRevA.108.013511 who plot a line of best fit in fig.4 that looks like it might be suspiciously close to averaging the Minkowski and Abraham results (about half the gradient of the Minkowski line shown). Weirdly, they don't seem to know about proposal (3), so don't mention the fact they seem to have evidence for it.

10. ^{^}

    "Flipping a photonic shock wave", Shuang Zhang and Xiang Zhang https://physics.aps.org/articles/v2/91#c1 

Discuss